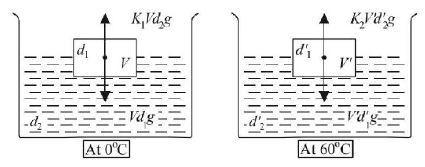
41. When a block of iron floats in mercury at $${0^ \circ }C,$$ fraction $${K_1}$$ of its volume is submerged, while at the temperature $${60^ \circ }C,$$ a fraction $${K_2}$$ is seen to be submerged. If the coefficient of volume expansion of iron is $${\gamma _{Fe}}$$ and that of mercury is $${{\gamma _{Hg}}},$$ then the ratio $$\frac{{{K_1}}}{{{K_2}}}$$ can be expressed as
A
$$\frac{{1 + 60{\gamma _{Fe}}}}{{1 + 60{\gamma _{Hg}}}}$$
B
$$\frac{{1 - 60{\gamma _{Fe}}}}{{1 + 60{\gamma _{Hg}}}}$$
C
$$\frac{{1 + 60{\gamma _{Fe}}}}{{1 - 60{\gamma _{Hg}}}}$$
D
$$\frac{{1 + 60{\gamma _{Hg}}}}{{1 + 60{\gamma _{Fe}}}}$$
Answer :
$$\frac{{1 + 60{\gamma _{Fe}}}}{{1 + 60{\gamma _{Hg}}}}$$
42. Helium gas is filled in a closed vessel (having negligible thermal expansion coefficient) when it is heated from $$300\,K$$ to $$600\,K,$$ then average kinetic energy of helium atom will be
A
$$\sqrt 2 \,{\text{times}}$$
B
2 times
C
unchanged
D
half
Answer :
2 times
43. Why does the pressure of an ideal gas increase when it is heated at constant volume ?
A
The gas molecules expand
B
The molecules move at the same speed, but hit the walls more often
C
The molecules move faster and hit the walls more often
D
The number of molecules of gas increases
Answer :
The molecules move faster and hit the walls more often
44. A mixture of 2 moles of helium gas (atomic mass = 4 amu) and 1 mole of argon gas (atomic mass = 40 amu) is kept at $$300\,K$$ in a container. The ratio of the rms speeds $$\left( {\frac{{{v_{rms}}\left( {{\text{helium}}} \right)}}{{{v_{rms}}\left( {{\text{argon}}} \right)}}} \right)$$ is
A
0.32
B
0.45
C
2.24
D
3.16
Answer :
3.16
45. Three containers of the same volume contain three different gases. The masses of the molecules are $${m_1},{m_2}$$ and $${m_3}$$ and the number of molecules in their respective containers are $${N_1},{N_2}$$ and $${N_3}.$$ The gas pressure in the containers are $${P_1},{P_2}$$ and $${P_3}$$ respectively. All the gases are now mixed and put in one of these containers. The pressure $$P$$ of the mixture will be
A
$$P < \left( {{P_1} + {P_2} + {P_3}} \right)$$
B
$$P = \frac{{{P_1} + {P_2} + {P_3}}}{3}$$
C
$$P = {P_1} + {P_2} + {P_3}$$
D
$$P > \left( {{P_1} + {P_2} + {P_3}} \right)$$
Answer :
$$P = {P_1} + {P_2} + {P_3}$$
46. Air is pumped into an automobile tube upto a pressure of $$200\,kPa$$ in the morning when the air temperature is $${22^ \circ }C.$$ During the day, temperature rises to $${42^ \circ }C$$ and the tube expands by $$2\% .$$ The pressure of the air in the tube at this temperature, will be approximately
A
$$212\,kPa$$
B
$$209\,kPa$$
C
$$206\,kPa$$
D
$$200\,kPa$$
Answer :
$$209\,kPa$$
47. A given sample of an ideal gas occupies a volume $$V$$ at a pressure $$p$$ and absolute temperature $$T.$$ The mass of each molecule of the gas is $$m.$$ Which of the following gives the density of the gas?
A
$$\frac{p}{{\left( {kT} \right)}}$$
B
$$\frac{{pm}}{{\left( {kT} \right)}}$$
C
$$\frac{p}{{\left( {kTV} \right)}}$$
D
$$mkT$$
Answer :
$$\frac{{pm}}{{\left( {kT} \right)}}$$
48. A polyatomic gas with $$n$$ degrees of freedom has a mean energy per molecule given by
A
$$\frac{{nkT}}{N}$$
B
$$\frac{{nkT}}{{2N}}$$
C
$$\frac{{nkT}}{2}$$
D
$$\frac{{3kT}}{2}$$
Answer :
$$\frac{{nkT}}{2}$$
49. The molar specific heats of an ideal gas at constant pressure and volume are denoted by $${C_p}$$ and $${C_v},$$ respectively. If $$\gamma = \frac{{{C_p}}}{{{C_v}}}$$ and $$R$$ is the universal gas constant, then $${{C_v}}$$ is equal to
A
$$\frac{R}{{\left( {\gamma - 1} \right)}}$$
B
$$\frac{{\left( {\gamma - 1} \right)}}{R}$$
C
$$\gamma R$$
D
$$\frac{{1 + \gamma }}{{1 - \gamma }}$$
Answer :
$$\frac{R}{{\left( {\gamma - 1} \right)}}$$
50. One mole of a diatomic gas is taken through the process $$P{V^n} = k,$$ where $$n$$ and $$k$$ are constant. If the heat capacity of gas is negative, then the value of $$n$$ may be
A
$$\frac{5}{7}$$
B
$$ - \frac{5}{7}$$
C
$$\frac{9}{7}$$
D
$$ - \frac{9}{7}$$
Answer :
$$\frac{9}{7}$$