1. If the temperature of the sun were to increase from $$T$$ to $$2\,T$$ and its radius from $$R$$ to $$2\,R,$$ then the ratio of the radiant energy received on earth to what it was previously will be
A
32
B
16
C
4
D
64
Answer :
64
2. According to Newton’s law of cooling, the rate of cooling of a body is proportional to $${\left( {\Delta \theta } \right)^n},$$ where $${\Delta \theta }$$ is the difference of the temperature of the body and the surroundings, and $$n$$ is equal to
A
two
B
three
C
four
D
one
Answer :
one
3. Two metallic spheres $${S_1}$$ and $${S_2}$$ are made of the same material and have got identical surface finish. The mass of $${S_1}$$ is thrice that of $${S_2}.$$ Both the spheres are heated to the same high temperature and placed in the same room having lower temperature but are thermally insulated from each other. The ratio of the initial rate of cooling of $${S_1}$$ to that of $${S_2}$$ is
A
$$\frac{1}{3}$$
B
$${\frac{1}{{\sqrt 3 }}}$$
C
$${\frac{{\sqrt 3 }}{1}}$$
D
$${\left( {\frac{1}{3}} \right)^{\frac{1}{3}}}$$
Answer :
$${\left( {\frac{1}{3}} \right)^{\frac{1}{3}}}$$
4. A black body at $${1227^ \circ }C$$ emits radiations with maximum intensity at a wavelength of $$5000\,\mathop A\limits^ \circ .$$ If the temperature of the body is increased by $${1000^ \circ }C,$$ the maximum intensity will be observed at
A
$$4000\,\mathop A\limits^ \circ $$
B
$$5000\,\mathop A\limits^ \circ $$
C
$$6000\,\mathop A\limits^ \circ $$
D
$$3000\,\mathop A\limits^ \circ $$
Answer :
$$3000\,\mathop A\limits^ \circ $$
5. Parallel rays of light of intensity $$I = 912\,W\,{m^{ - 2}}$$ are incident on a spherical black body kept in surroundings of temperature $$300\,K.$$ Take Stefan-Boltzmann constant $$\sigma = 5.7 \times {10^{ - 8}}\,W\,{m^{ - 2}}{K^{ - 4}}$$ and assume that the energy exchange with the surroundings is only through radiation. The final steady state temperature of the black body is close to
A
$$330 \,K$$
B
$$660 \,K$$
C
$$990 \,K$$
D
$$1550 \,K$$
Answer :
$$330 \,K$$
6. The earth radiates in the infra-red region of the spectrum. The spectrum is correctly given by
A
Rayleigh Jeans law
B
Planck’s law of radiation
C
Stefan’s law of radiation
D
Wien’s law
Answer :
Wien’s law
7. Consider two hot bodies $${B_1}$$ and $${B_2}$$ which have temperatures $${100^ \circ }C$$ and $${80^ \circ }C$$ respectively at $$t = 0.$$ The temperature of the surroundings is $${40^ \circ }C.$$ The ratio of the respective rates of cooling $${R_1}$$ and $${R_2}$$ of these two bodies at $$t = 0$$ will be
A
$${R_1}:{R_2} = 3:2$$
B
$${R_1}:{R_2} = 5:4$$
C
$${R_1}:{R_2} = 2:3$$
D
$${R_1}:{R_2} = 4:5$$
Answer :
$${R_1}:{R_2} = 3:2$$
8. Wien’s displacement law expresses relation between
A
wavelength corresponding to maximum energy and absolute temperature
B
radiated energy and wavelength
C
emissive power and temperature
D
colour of light and temperature
Answer :
wavelength corresponding to maximum energy and absolute temperature
9. A black body is at a temperature of $$5760\,K.$$ The energy of radiation emitted by the body at wavelength $$250\,nm$$ is $${U_1},$$ at wavelength $$500\,nm$$ is $${U_2}$$ and that at $$1000\,nm$$ is $${U_3}.$$ Wien’s constant, $$b = 2.88 \times {10^6}nmK.$$ Which of the following is correct?
A
$${U_3} = 0$$
B
$${U_1} > {U_2}$$
C
$${U_2} > {U_1}$$
D
$${U_1} = 0$$
Answer :
$${U_2} > {U_1}$$
10. A liquid in a beaker has temperature $$\theta \left( t \right)$$ at time $$t$$ and $${{\theta _0}}$$ is temperature of surroundings, then according to Newton's law of cooling the correct graph between $${\log _e}\left( {\theta - {\theta _0}} \right)$$ and $$t$$ is:
A
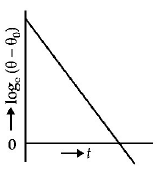

B
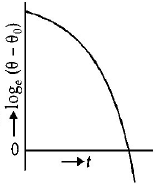

C
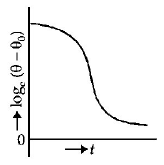

D
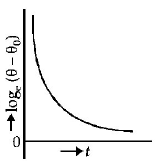

Answer :

