31. A spherical body of area $$A$$ and emissivity $$e = 0.6$$ is kept inside a perfectly black body. Total heat radiated by the body at temperature $$T$$
A
$$0.4\,A{T^4}$$
B
$$0.8\,A{T^4}$$
C
$$0.6\,A{T^4}$$
D
$$1.0\,A{T^4}$$
Answer :
$$1.0\,A{T^4}$$
32. A metal ball of surface area $$200$$ square $$cm,$$ temperature $${527^ \circ }C$$ is surrounded by a vessel at $${27^ \circ }C.$$ If the emissivity of the metal is $$0.4,$$ then the rate of loss of heat from the ball is approximately $$\left[ {\sigma = 5.67 \times {{10}^{ - 8}}\frac{{joule}}{{{m^2} \times \sec \times {K^2}}}} \right]$$
A
108 joule
B
168 joule
C
182 joule
D
192 joule
Answer :
182 joule
33. A piece of iron is heated in a flame. If first becomes dull red then becomes reddish yellow and finally turns to white hot. The correct explanation for the above observation is possible by using
A
Stefan’s law
B
Wien’s displacement law
C
Kirchhoff’s law
D
Newton's law of cooling
Answer :
Wien’s displacement law
34. A container contains hot water at $${100^ \circ }C.$$ If in time $${T_1}$$ temperature falls to $${80^ \circ }C$$ and the time $${T_2}$$ temperature falls to $${60^ \circ }C$$ form $${80^ \circ }C,$$ then
A
$${T_1} = {T_2}$$
B
$${T_1} > {T_2}$$
C
$${T_1} < {T_2}$$
D
None of these
Answer :
$${T_1} < {T_2}$$
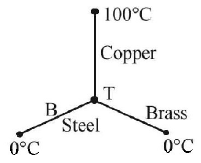
35. Three rods of Copper, Brass and Steel are welded together to form a $$Y$$ shaped structure. Area of cross-section of each rod $$ = 4\,c{m^2}.$$ End of copper rod is maintained at $${100^ \circ }C$$ where as ends of brass and steel are kept at $${0^ \circ }C.$$ Lengths of the copper, brass and steel rods are $$46, 13$$ and $$12\,cms$$ respectively. The rods are thermally insulated from surroundings excepts at ends. Thermal conductivities of copper, brass and steel are $$0.92, 0.26$$ and $$0.12\,CGS$$ units respectively. Rate of heat flow through copper rod is:
A
$$1.2\,\,cal/s$$
B
$$2.4\,\,cal/s$$
C
$$4.8\,\,cal/s$$
D
$$6.0\,\,cal/s$$
Answer :
$$4.8\,\,cal/s$$
36. On observing light from three different stars $$P,Q$$ and $$R,$$ it was found that intensity of violet colour is maximum in the spectrum of $$P,$$ the intensity of green colour is maximum in the spectrum of $$R$$ and the intensity of red colour is maximum in the spectrum of $$Q.$$ If $${T_P},{T_Q}$$ and $${T_R}$$ are the respective absolute temperatures of $$P,Q$$ and $$R,$$ then it can be concluded from the above observations that
A
$${T_P} > {T_Q} > {T_R}$$
B
$${T_P} > {T_R} > {T_Q}$$
C
$${T_P} < {T_R} < {T_Q}$$
D
$${T_P} < {T_Q} < {T_R}$$
Answer :
$${T_P} > {T_R} > {T_Q}$$
37. Consider a spherical shell of radius $$R$$ at temperature $$T.$$ The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume $$u = \frac{U}{V}\,\propto \,{T^4}$$ and pressure $$P = \frac{1}{3}\left( {\frac{U}{V}} \right).$$ If the shell now undergoes an adiabatic expansion the relation between $$T$$ and $$R$$ is:
A
$${\text{ }}T\,\propto \,\frac{1}{R}$$
B
$${\text{ }}T\,\propto \,\frac{1}{R_3}$$
C
$${\text{ }}T\,\propto \,{e^{ - R}}$$
D
$${\text{ }}T\,\propto \,{e^{ - 3R}}$$
Answer :
$${\text{ }}T\,\propto \,\frac{1}{R}$$
38. The radiant energy from the sun, incident normally at the surface of earth is $$20\,kcal/{m^2}\min .$$ What would have been the radiant energy, incident normally on the earth, if the sun had a temperature, twice of the present one ?
A
$$160\,kcal/{m^2}\min $$
B
$$40\,kcal/{m^2}\min $$
C
$$320\,kcal/{m^2}\min $$
D
$$80\,kcal/{m^2}\min $$
Answer :
$$320\,kcal/{m^2}\min $$
39. The rectangular surface of area $$8\,cm \times 4\,cm$$ of a black body at temperature $${127^ \circ }C$$ emits energy $$E$$ per second. If the length and breadth are reduced to half of the initial value and the temperature is raised to $${327^ \circ }C,$$ the rate of emission of energy becomes
A
$$\frac{3}{8}E$$
B
$$\frac{81}{16}E$$
C
$$\frac{9}{16}E$$
D
$$\frac{81}{64}E$$
Answer :
$$\frac{81}{64}E$$
40. We consider the radiation emitted by the human body. Which of the following statements is true ?
A
The radiation is emitted during the summers and absorbed during the winters
B
The radiation emitted lies in the ultraviolet region and hence is not visible
C
The radiation emitted is in the infrared region
D
The radiation is emitted only during the day
Answer :
The radiation emitted is in the infrared region