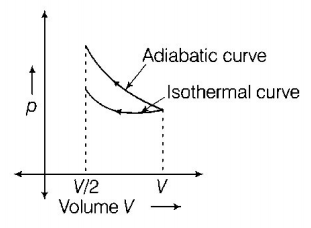
11.
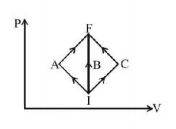
In the $$P-V$$ diagram, $$I$$ is the initial state and $$F$$ is the final state. The gas goes from $$I$$ to $$F$$ by (i) $$IAF,$$ (ii) $$IBE,$$ (iii) $$ICF.$$ The heat absorbed by the gas is
A
the same in all three processes
B
the same in (i) and (ii)
C
greater in (i) than in (ii)
D
the same in (i) and (iii)
Answer :
greater in (i) than in (ii)
12. Which of the following graphs correctly represents the variation $$\beta = - \frac{{\frac{{dV}}{{dP}}}}{V}$$ with $$P$$ for an ideal gas at constant temperature ?
A
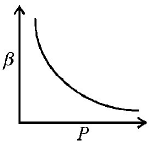

B
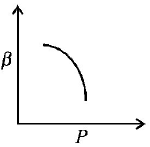

C
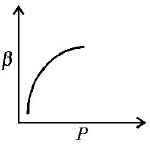

D
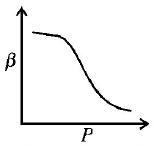

Answer :


13.
The change in internal energy of a thermo-dynamical system which has absorbed $$2\,kcal$$ of heat and done $$400\,J$$ of work is
$$\left( {1\,cal = 4.2\,J} \right)$$
A
$$2\,kJ$$
B
$$8\,kJ$$
C
$$3.5\,kJ$$
D
$$5.5\,kJ$$
Answer :
$$8\,kJ$$
14. A Carnot engine operating between temperatures $${T_1}$$ and $${T_2}$$ has efficiency $$\frac{1}{6}.$$ When $${T_2}$$ is lowered by $$62\,K$$ its efficiency increases to $$\frac{1}{3}.$$ Then $${T_1}$$ and $${T_2}$$ are, respectively
A
$$372\,K$$ and $$330\,K$$
B
$$330\,K$$ and $$268\,K$$
C
$$310\,K$$ and $$248\,K$$
D
$$372\,K$$ and $$310\,K$$
Answer :
$$372\,K$$ and $$310\,K$$
15. $$4\,kg$$ of oxygen gas is heated so as to raise its temperature from 20 to $${120^ \circ }C.$$ If the heating is done at constant pressure, the external work done by the gas is ($${C_p} = 0.219\,cal/{g^ \circ }C$$ and $${C_v} = 0.157\,cal/{g^ \circ }C$$ )
A
$$628\,kJ$$
B
$$104\,kJ$$
C
$$366\,kJ$$
D
$$206\,kJ$$
Answer :
$$104\,kJ$$
16. A gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then
A
compressing the gas through adiabatic process will require more work to be done.
B
compressing the gas isothermally or adiabatically will require the same amount of work.
C
which of the case (whether compression through isothermal or through adiabatic process) requires more work will depend upon the atomicity of the gas.
D
compressing the gas isothermally will require more work to be done.
Answer :
compressing the gas through adiabatic process will require more work to be done.
17. An ideal gas is initially at $${P_1},{V_1}$$ is expanded to $${P_2},{V_2}$$ and then compressed adiabatically to the same volume $${V_1}$$ and pressure $${P_3}.$$ If $$W$$ is the net work done by the gas in complete process which of the following is true?
A
$$W > 0;{P_3} > {P_1}$$
B
$$W < 0;{P_3} > {P_1}$$
C
$$W > 0;{P_3} < {P_1}$$
D
$$W < 0;{P_3} < {P_1}$$
Answer :
$$W < 0;{P_3} > {P_1}$$
18. A Carnot engine whose efficiency is $$50\% $$ has an exhaust temperature of $$500\,K.$$ If the efficiency is to be $$60\% $$ with the same intake temperature, the exhaust temperature must be (in $$K$$)
A
800
B
200
C
400
D
600
Answer :
400
19. 1 mole of a gas with $$\gamma = \frac{7}{5}$$ is mixed with 1 mole of a gas with $$\gamma = \frac{5}{3},$$ then the value of $$\gamma $$ for the resulting mixture is
A
$$\frac{7}{5}$$
B
$$\frac{2}{5}$$
C
$$\frac{24}{16}$$
D
$$\frac{12}{7}$$
Answer :
$$\frac{24}{16}$$
20. If the ratio of specific heat of a gas at constant pressure to that at constant volume is $$\gamma ,$$ the change in internal energy of a mass of gas when the volume changes from $$V$$ to $$2V$$ at constant pressure $$p$$ is
A
$$\frac{R}{{\left( {\gamma - 1} \right)}}$$
B
$$pV$$
C
$$\frac{{pV}}{{\left( {\gamma - 1} \right)}}$$
D
$$\frac{{\gamma pV}}{{\left( {\gamma - 1} \right)}}$$
Answer :
$$\frac{{pV}}{{\left( {\gamma - 1} \right)}}$$