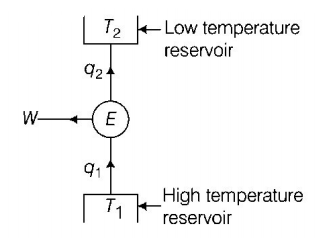
51. In a Carnot engine, the temperature of reservoir is $${927^ \circ }C$$ and that of sink is $${27^ \circ }C.$$ If the work done by the engine when it transfers heat from reservoir to sink is $$12.6 \times {10^6}J,$$ the quantity of heat absorbed by the engine from the reservoir is
A
$$16.8 \times {10^6}J,$$
B
$$4 \times {10^6}J,$$
C
$$7.6 \times {10^6}J,$$
D
$$4.2 \times {10^6}J,$$
Answer :
$$16.8 \times {10^6}J,$$
52. A Carnot engine having an efficiency of $$\frac{1}{{10}}$$ as heat engine, is used as a refrigerator. If the work done on the system is $$10\,J,$$ the amount of energy absorbed from the reservoir at lower temperature is
A
$$1\,J$$
B
$$90\,J$$
C
$$99\,J$$
D
$$100\,J$$
Answer :
$$90\,J$$
53. Which of the following processes is irreversible?
A
Transfer of heat by radiation
B
Adiabatic changes performed slowly
C
Extremely slow extension of a spring
D
Isothermal changes performed slowly
Answer :
Transfer of heat by radiation
54. During an isothermal expansion, a confined ideal gas does $$-150\,J$$ of work against its surroundings. This implies that
A
$$300\,J$$ of heat has been added to the gas
B
no heat is transferred because the process is isothermal
C
$$150\,J$$ of heat has been added to the gas
D
$$150\,J$$ of heat has been removed from the gas
Answer :
$$150\,J$$ of heat has been added to the gas
55. Unit mass of a liquid with volume $${V_1}$$ is completely changed into a gas of volume $${V_2}$$ at a constant external pressure $$P$$ and temperature $$T.$$ If the latent heat of evaporation for the given mass is $$L,$$ then the increase in the internal energy of the system is
A
Zero
B
$$P\left( {{V_2} - {V_1}} \right)$$
C
$$L - P\left( {{V_2} - {V_1}} \right)$$
D
$$L$$
Answer :
$$L - P\left( {{V_2} - {V_1}} \right)$$
56.
A gas is expanded from volume $${V_0}$$ to $$2{V_0}$$ under three different processes. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic.
Let $$\Delta {U_1},\Delta {U_2}$$ and $$\Delta {U_3}$$ be the change in internal energy of the gas is these three processes. Then -
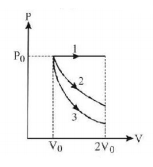
A
$$\Delta {U_1} > \Delta {U_2} > \Delta {U_3}$$
B
$$\Delta {U_1} < \Delta {U_2} < \Delta {U_3}$$
C
$$\Delta {U_2} < \Delta {U_1} < \Delta {U_3}$$
D
$$\Delta {U_2} < \Delta {U_3} < \Delta {U_1}$$
Answer :
$$\Delta {U_1} > \Delta {U_2} > \Delta {U_3}$$
57. “Heat cannot by it self flow from a body at lower temperature to a body at higher temperature” is a statement or consequence of
A
second law of thermodynamics
B
conservation of momentum
C
conservation of mass
D
first law of thermodynamics
Answer :
second law of thermodynamics
58.
For an ideal gas four processes are marked as 1,2,3 and 4 on $$P-V$$ diagram as shown in figure. The amount of heat supplied to the gas in the process 1, 2, 3 and 4 are $${Q_1},{Q_2},{Q_3}$$ and $${Q_4}$$ respectively, then correct order of heat supplied to the gas is - [$$AB$$ is process-1, $$AC$$ is process-2, $$AD$$ is adiabatic process-3 and $$AE$$ is process-4]
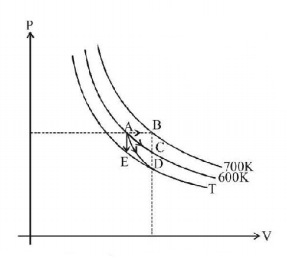
A
$${Q_1} > {Q_2} > {Q_3} > {Q_4}$$
B
$${Q_1} > {Q_2} > {Q_4} > {Q_3}$$
C
$${Q_1} > {Q_4} > {Q_2} > {Q_3}$$
D
$${Q_1} < {Q_2} < {Q_3} < {Q_4}$$
Answer :
$${Q_1} > {Q_2} > {Q_4} > {Q_3}$$
59. An ideal gas undergoes a quasi static, reversible process in which its molar heat capacity $$C$$ remains constant. If during this process the relation of pressure $$P$$ and volume $$V$$ is given by $$P{V^n}$$ = constant, then $$n$$ is given by (Here $${C_P}$$ and $${C_V}$$ are molar specific heat at constant pressure and constant volume, respectively):
A
$$n = \frac{{{C_P} - C}}{{C - {C_V}}}\,$$
B
$$n = \frac{{C - {C_V}}}{{C - {C_P}}}\,$$
C
$$n = \frac{{{C_P}}}{{{C_V}}}\,$$
D
$$n = \frac{{C - {C_P}}}{{C - {C_V}}}\,$$
Answer :
$$n = \frac{{C - {C_P}}}{{C - {C_V}}}\,$$
60. A monoatomic gas at a pressure $$p,$$ having a volume $$V$$ expands isothermally to a volume $$2 V$$ and then adiabatically to a volume $$16 V.$$ The final pressure of the gas is (take $$\gamma = \frac{5}{3}$$ )
A
$$64\,p$$
B
$$32\,p$$
C
$$\frac{p}{{64}}$$
D
$$16\,p$$
Answer :
$$\frac{p}{{64}}$$