71.
One mole of an ideal gas is taken from state $$A$$ to state $$B$$ by three different processes, (i) $$ACB$$ (ii) $$ADB$$ (iii) $$AEB$$ as shown in the $$P-V$$ diagram. The heat absorbed by the gas is -
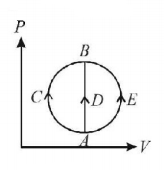
A
greater in process (ii) than in (i)
B
the least in process (ii)
C
the same in (i) and (iii)
D
less in (iii) than in (ii)
Answer :
less in (iii) than in (ii)
72.
In $$P-V$$ diagram shown in figure $$ABC$$ is a semicircle. The work done in the process $$ABC$$ is
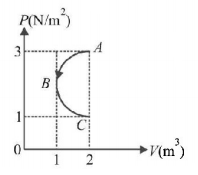
A
$$4\,J$$
B
$$\frac{{ - \pi }}{2}J$$
C
$$\frac{\pi }{2}J$$
D
zero
Answer :
$$\frac{\pi }{2}J$$
73. $$2\,k mol$$ of hydrogen at $$NTP$$ expands isobarically to twice its initial volume. The change in its internal energy is ($${C_v} = 10\,kJ/kg.K$$ and atm pressure $$ = 1 \times {10^5}\,N/{m^2}$$ )
A
$$10.9\,MJ$$
B
$$9.10\,MJ$$
C
$$109\,MJ$$
D
$$1.09\,MJ$$
Answer :
$$10.9\,MJ$$
74.
An ideal monatomic gas is taken round the cycle $$ABCDA$$ as shown in the $$P - V$$ diagram (see Fig.). The work done during the cycle is
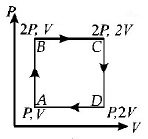
A
$$PV$$
B
$$2PV$$
C
$$\frac{1}{2}PV$$
D
zero
Answer :
$$PV$$
75. The temperature of an open room of volume $$30\,{m^3}$$ increases from $${17^ \circ }C$$ to $${27^ \circ }C$$ due to sunshine. The atmospheric pressure in the room remains $$1 \times {10^5}\,Pa.$$ If $${n_i}$$ and $${n_f}$$ are the number of molecules in the room before and after heating, then $${n_f} - {n_i}$$ will be:
A
$$2.5 \times {10^{25}}$$
B
$$ - 2.5 \times {10^{25}}$$
C
$$ - 1.61 \times {10^{23}}$$
D
$$1.38 \times {10^{23}}$$
Answer :
$$ - 2.5 \times {10^{25}}$$
76. If the co-efficient of performance of a refrigerator is 5 and operates at the room temperature $${27^ \circ }C,$$ the temperature inside the refrigerator is
A
$$240\,K$$
B
$$250\,K$$
C
$$230\,K$$
D
$$260\,K$$
Answer :
$$250\,K$$
77.
When a system is taken from state $$i$$ to state $$f$$ along the path iaf, it is found that $$Q = 50\,cal.$$ and $$W = 20\,cal.$$ Along the path
ibf $$Q = 36\,cal.$$ $$W$$ along the path ibf is
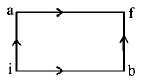
A
$$14\,cal$$
B
$$6\,cal$$
C
$$16\,cal$$
D
$$66\,cal$$
Answer :
$$6\,cal$$
78. At $${27^ \circ }C$$ a gas is compressed suddenly such that its pressure becomes $$\left( {\frac{1}{8}} \right)$$ of original pressure. Final temperature will be $$\left( {\gamma = \frac{5}{3}} \right)$$
A
$$420\,K$$
B
$$300\,K$$
C
$${-142^ \circ }C$$
D
$$327\,K$$
Answer :
$${-142^ \circ }C$$
79. When an ideal monoatomic gas is heated at constant pressure, the fraction of the heat energy supplied which increases the internal energy of the gas is
A
$$\frac{2}{5}$$
B
$$\frac{3}{5}$$
C
$$\frac{3}{7}$$
D
$$\frac{5}{7}$$
Answer :
$$\frac{3}{5}$$
80. The efficiency of a Carnot engine operating between temperatures of $${100^ \circ }C$$ and $${-23^ \circ }C$$ will be
A
$$\frac{{100 - 23}}{{273}}$$
B
$$\frac{{100 + 23}}{{373}}$$
C
$$\frac{{100 + 23}}{{100}}$$
D
$$\frac{{100 - 23}}{{100}}$$
Answer :
$$\frac{{100 + 23}}{{373}}$$