151.
A Geigger Muller counter is used to study the radioactive process. In the absence of radioactive substance $$A,$$ it counts 3 disintegration per second $$(dps).$$ At the start in the presence of $$A,$$ it records $$23\,dps;$$ and after $$10\,\min \,13\,dps,$$
(i) What does it count after $$20\,\min $$
(ii) What is the half life of $$A?$$
A
$$8\,dps,10\,\min $$
B
$$5\,dps,10\,\min $$
C
$$5\,dps,20\,\min $$
D
$$5\,dps,5\,\min $$
Answer :
$$8\,dps,10\,\min $$
152.
Which of the following options does not show instantaneous rate of reaction at 40th second?
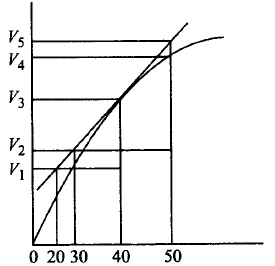
A
$$\frac{{{V_5} - {V_2}}}{{50 - 30}}$$
B
$$\frac{{{V_4} - {V_2}}}{{50 - 30}}$$
C
$$\frac{{{V_3} - {V_2}}}{{40 - 30}}$$
D
$$\frac{{{V_3} - {V_1}}}{{40 - 20}}$$
Answer :
$$\frac{{{V_4} - {V_2}}}{{50 - 30}}$$
153. For the elementary reaction $$M → N,$$ the rate of disappearance of $$M$$ increases by a factor of 8 upon doubling the concentration of $$M.$$ The order of the reaction with respect to $$M$$ is
A
4
B
3
C
2
D
1
Answer :
3
154. For the reaction $$2N{H_3} \to {N_2} + 3{H_2},$$ if $$ - \frac{{d\left[ {N{H_3}} \right]}}{{dt}} = {k_1}\left[ {N{H_3}} \right],$$ $$\frac{{d\left[ {{N_2}} \right]}}{{dt}} = {k_2}\left[ {N{H_3}} \right],$$ $$\frac{{d\left[ {{H_2}} \right]}}{{dt}} = {k_3}\left[ {N{H_3}} \right]$$ then the relation between $${k_1},{k_2}$$ and $${k_3}$$ is
A
$${k_1} = {k_2} = {k_3}$$
B
$${k_1} = 3{k_2} = 2{k_3}$$
C
$$1.5{k_1} = 3{k_2} = {k_3}$$
D
$$2{k_1} = {k_2} = 3{k_3}$$
Answer :
$$1.5{k_1} = 3{k_2} = {k_3}$$
155. For a chemical reaction, $$X \to Y,$$ the rate of reaction increases by a factor of 1.837 when the concentration of $$X$$ is increased by 1.5 times, the order of the reaction with respect to $$X$$ is
A
1
B
1.5
C
2
D
2.5
Answer :
1.5
156. Which one of the following statement for order of reaction is not correct?
A
Order can be determined experimentally
B
Order of reaction is equal to sum of the powers of concentration terms in differential rate law.
C
It is not affected with the stoichiometric coefficient of the reactants
D
Order cannot be fractional.
Answer :
Order cannot be fractional.
157.
The following results were obtained during kinetic studies of the reaction ;
| $$2A + B\,\,\,\,{\text{Products}}$$ | |||
| Experiment | $$\left[ A \right]\left( {{\text{in}}\,mol\,{L^{ - 1}}} \right)$$ | $$\left[ B \right]\left( {{\text{in}}\,mol\,{L^{ - 1}}} \right)$$ | Initial Rate of reaction $$\left( {{\text{in}}\,mol\,{L^{ - 1}}\,{{\min }^{ - 1}}} \right)$$ |
|---|---|---|---|
| I | 0.10 | 0.20 | $$6.93 \times {10^{ - 3}}$$ |
| II | 0.10 | 0.25 | $$6.93 \times {10^{ - 3}}$$ |
| III | 0.20 | 0.30 | $$1.386 \times {10^{ - 2}}$$ |
A
5
B
10
C
1
D
100
Answer :
5
158. Activation energy of a chemical reaction can be determined by
A
evaluating rate constant at standard temperature
B
evaluating velocities of reaction at two different temperatures
C
evaluating rate constants at two different temperatures
D
changing concentration of reactants
Answer :
evaluating rate constants at two different temperatures
159. The time required for $$10\% $$ completion of a first order reaction at 298$$\,K$$ is equal to that required for its $$25\% $$ completion at 308$$\,K.$$ If the preexponential factor for the reaction is $$3.56 \times {10^9}{s^{ - 1}},$$ the rate constant at $$318\,K$$ is :
A
$$18.39\,kcal\,mo{l^{ - 1}}$$
B
$$20\,kcal\,mo{l^{ - 1}}$$
C
$$16\,kcal\,mo{l^{ - 1}}$$
D
$$21.5\,kcal\,mo{l^{ - 1}}$$
Answer :
$$18.39\,kcal\,mo{l^{ - 1}}$$
160. In respect of the equation $$k = A{e^{\frac{{ - {E_a}}}{{RT}}}}$$ in chemical kinetics, which one of the following statements is correct ?
A
$$A$$ is adsorption factor
B
$${E_a}$$ is energy of activation
C
$$R$$ is Rydberg’s constant
D
$$k$$ is equilibrium constant
Answer :
$${E_a}$$ is energy of activation