241. Which of the following will react at the highest rate?
A
$$1{\text{ }}mole$$ of $$A$$ and $$1{\text{ }}mole$$ of $$B$$ in a $$1{\text{ - }}L$$ vessel
B
$$2{\text{ }}mole$$ of $$A$$ and $$2{\text{ }}mole$$ of $$B$$ in a $$2{\text{ - }}L$$ vessel
C
$$3{\text{ }}mole$$ of $$A$$ and $$3{\text{ }}mole$$ of $$B$$ in a $$3{\text{ - }}L$$ vessel
D
All would react at the same rate
Answer :
All would react at the same rate
242.
For an exothermic chemical reaction occurring two steps as
$$\eqalign{
& \left( {\text{i}} \right)A + B \to X\left( {{\text{slow}}} \right) \cr
& \left( {{\text{ii}}} \right)X \to AB\left( {{\text{fast}}} \right) \cr} $$
The progress of the reaction can be best described by
A
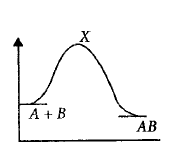

B
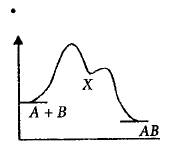

C
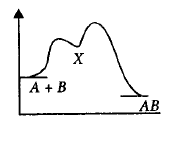

D


Answer :


243.
The hypothetical reaction $${A_2} + {B_2} \to 2AB;$$ follows the following mechanism \[{{A}_{2}}\xrightarrow{\text{Fast}}A+A,\] \[A+{{B}_{2}}\xrightarrow{\text{Slow}}AB+B,A+B\xrightarrow{\text{Fast}}AB\cdot \]
The order of the overall reaction is
A
$$0$$
B
$$1$$
C
$$2$$
D
$$\frac{3}{2}$$
Answer :
$$\frac{3}{2}$$
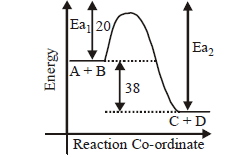
244.
The activation energy of the reaction, $$A + B \to C + D + 38\,kcal$$ is $$20\,kcal.$$ What would be the activation energy of the following reaction.
$$C + D \to A + B$$
A
20$$\,kcal$$
B
- 20$$\,kcal$$
C
18$$\,kcal$$
D
58$$\,kcal$$
Answer :
58$$\,kcal$$
245.
Find the values of $$A, B$$ and $$C$$ in the following table for the reaction $$X + Y \to Z.$$ The reaction is of first order $$w.r.t$$ $$X$$ and zero order $$w.r.t.$$ $$Y.$$
A
$$A = 0.2\,mol\,{L^{ - 1}},$$ $$B = 8 \times {10^{ - 2}}\,mol\,{L^{ - 1}}\,{s^{ - 1}},$$ $$C = 0.1\,mol\,{L^{ - 1}}$$
B
$$A = 0.4\,mol\,{L^{ - 1}},$$ $$B = 4 \times {10^{ - 2}}\,mol\,{L^{ - 1}}\,{s^{ - 1}},$$ $$C = 0.2\,mol\,{L^{ - 1}}$$
C
$$A = 0.2\,mol\,{L^{ - 1}},$$ $$B = 2 \times {10^{ - 2}}\,mol\,{L^{ - 1}}{s^{ - 1}},$$ $$C = 0.4\,mol{L^{ - 1}}$$
D
$$A = 0.4\,mol\,{L^{ - 1}},$$ $$B = 2 \times {10^{ - 2}}\,mol\,{L^{ - 1}}\,{s^{ - 1}},$$ $$C = 0.4\,mol\,{L^{ - 1}}$$
Answer :
$$A = 0.2\,mol\,{L^{ - 1}},$$ $$B = 8 \times {10^{ - 2}}\,mol\,{L^{ - 1}}\,{s^{ - 1}},$$ $$C = 0.1\,mol\,{L^{ - 1}}$$
246.
The rate of the reaction : $$C{H_3}COO{C_2}{H_5} + NaOH \to $$ $$C{H_3}COONa + {C_2}{H_5}OH$$ is given by the equation, $${\text{rate}} = k\left[ {C{H_3}COO{C_2}{H_5}} \right]\left[ {NaOH} \right]$$
If concentration is expressed in $$mol/L,$$ the units of $$k$$ are
A
$$mo{l^{ - 2}}\,{L^2}\,{s^{ - 1}}$$
B
$$mol\,{L^{ - 1}}\,{s^{ - 1}}$$
C
$$L\,mo{l^{ - 1}}\,{s^{ - 1}}$$
D
$${s^{ - 1}}$$
Answer :
$$L\,mo{l^{ - 1}}\,{s^{ - 1}}$$
247. A reaction having equal energies of activation for forward and reverse reaction has :
A
$$\Delta G = 0$$
B
$$\Delta H = 0$$
C
$$\Delta H = \Delta G = \Delta S = 0$$
D
$$\Delta S = 0$$
Answer :
$$\Delta H = 0$$
248. If the rate of a reaction is equal to the rate constant, the order of the reaction is
A
2
B
3
C
0
D
1
Answer :
0
249. For the reaction, $${N_2}{O_5}\left( g \right) \to 2N{O_2}\left( g \right) + \frac{1}{2}{O_2}\left( g \right)$$ The value of rate of disappearance of $${N_2}{O_5}$$ is given as $$6.25 \times {10^{ - 3}}mol\,{L^{ - 1}}{s^{ - 1}}.$$ The rate of formation of $$N{O_2}$$ and $${O_2}$$ is given respectively as
A
$$6.25 \times {10^{ - 3}}mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}}\,6.25 \times {10^{ - 3}}mol\,{L^{ - 1}}{s^{ - 1}}$$
B
$$1.25 \times {10^{ - 2}}mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}}\,3.125 \times {10^{ - 3}}mol\,{L^{ - 1}}{s^{ - 1}}$$
C
$$6.25 \times {10^{ - 3}}mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}}\,3.125 \times {10^{ - 3}}mol\,{L^{ - 1}}{s^{ - 1}}$$
D
$$1.25 \times {10^{ - 2}}mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}}\,6.25 \times {10^{ - 3}}mol\,{L^{ - 1}}{s^{ - 1}}$$
Answer :
$$1.25 \times {10^{ - 2}}mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}}\,3.125 \times {10^{ - 3}}mol\,{L^{ - 1}}{s^{ - 1}}$$
250. For the reaction system : $$2NO\left( g \right) + {O_2}\left( g \right) \to 2\,N{O_2}\left( g \right)$$ volume is suddenly reduced to half its value by increasing the pressure on it. If the reaction is of first order with respect to $${O_2}$$ and second order with respect to $$NO,$$ the rate of reaction will
A
diminish to one-eighth of its initial value
B
increase to eight times of its initial value
C
increase to four times of its initial value
D
diminish to one-fourth of its initial value
Answer :
increase to eight times of its initial value