281. A heat engine abosrbs heat $${Q_1}$$ at temperature $${T_1}$$ and heat $${Q_2}$$ at temperature $${T_2}$$ Work done by the engine is $$J\left( {{Q_1} + {Q_2}} \right).$$ This data
A
violates 1st law of thermodynamics
B
violates 1st law of themodynamics if $${{Q_1}}$$ is $$-ve$$
C
violates 1st law of thermodynamics of $${{Q_2}}$$ is $$-ve$$
D
does not violate 1st law of themodynamics.
Answer :
violates 1st law of thermodynamics
282.
Formation of ammonia is shown by the reaction, $${N_{2\left( g \right)}} + 3{H_{2\left( g \right)}} \to 2N{H_{3\left( g \right)}};{\Delta _r}{H^ \circ } = - 91.8\,kJ\,mo{l^{ - 1}}$$
What will be the enthalpy of reaction for the decomposition of $$N{H_3}$$ according to the reaction ?
$$2N{H_{3\left( g \right)}} \to {N_{2\left( g \right)}} + 3{H_{2\left( g \right)}};{\Delta _r}{H^ \circ } = ?$$
A
$$ - 91.8\,kJ\,mo{l^{ - 1}}$$
B
$$ + 91.8\,kJ\,mo{l^{ - 1}}$$
C
$$ - 45.9\,kJ\,mo{l^{ - 1}}$$
D
$$ + 45.9\,kJ\,mo{l^{ - 1}}$$
Answer :
$$ + 91.8\,kJ\,mo{l^{ - 1}}$$
283. The heat required to raise the temperature of body by $$1 K$$ is called
A
specific heat
B
thermal capacity
C
water equivalent
D
none of these.
Answer :
thermal capacity
284. The correct relationship between free energy and equilibrium constant $$K$$ of a reaction is
A
$$\Delta {G^ \circ } = - RT\,\ln \,K$$
B
$$\Delta G = RT\,\ln \,K$$
C
$$\Delta {G^ \circ } = RT\,\ln \,K$$
D
$$\Delta G = - RT\,\ln \,K$$
Answer :
$$\Delta {G^ \circ } = - RT\,\ln \,K$$
285.
On the basis of the following thermochemical data :
$$\left( {{\Delta _f}{G^ \circ }H_{\left( {aq} \right)}^ + = 0} \right)$$
$${H_2}O\left( \ell \right) \to {H^ + }\left( {aq} \right) + O{H^ - }\left( {aq} \right)\,;$$ $$\Delta H = 57.32\,kJ$$
$${H_2}\left( g \right) + \frac{1}{2}{O_2}\left( g \right) \to {H_2}O\left( \ell \right)\,;$$ $$\Delta H = - 286.20\,kJ$$
The value of enthalpy of formation of $$O{H^ - }$$ ion at $${25^ \circ }C$$ is:
A
$$- 228.88\,kJ$$
B
$$+228.88\,kJ$$
C
$$-343.52\,kJ$$
D
$$-22.88\,kJ$$
Answer :
$$- 228.88\,kJ$$
286. In a closed insulated container a liquid is stirred with a paddle to increase the temperature, which of the following is true?
A
$$\Delta E = W \ne 0,\,q = 0$$
B
$$\Delta E = W = 0,q \ne 0$$
C
$$\Delta E = 0,W = q \ne 0$$
D
$$W = 0,\Delta E = q \ne 0$$
Answer :
$$\Delta E = W \ne 0,\,q = 0$$
287. The enthalpy and entropy change for the reaction, $$B{r_2}\left( l \right) + C{l_2}\left( g \right) \to 2\,BrCl\left( g \right)$$ are $$30\,kJ\,mo{l^{ - 1}}$$ and $$105\,J{K^{ - 1}}\,mo{l^{ - 1}}$$ respectively. The temperature at which the reaction will be in equilibrium is
A
285.7$$\,K$$
B
273$$\,K$$
C
450$$\,K$$
D
300$$\,K$$
Answer :
285.7$$\,K$$
288. $$2\,moles$$ of an ideal gas at $${27^ \circ }C$$ temperature is expanded reversibly from $$2\,L$$ to $$20\,L.$$ Find entropy change $$\left( {R = 2\,cal/mol\,K} \right)$$
A
92.1
B
0
C
4
D
9.2
Answer :
9.2
289.
If at $$298 K$$ the bond energies of $$C - H,$$ $$C - C,$$ $$C=C$$ and $$H - H$$ bonds are respectively 414, 347, 615 and $$435kJ\,mo{l^{ - 1}},$$ the value of enthalpy change for the reaction
$${H_2}C = C{H_2}\left( g \right) + {H_2}\left( g \right) \to {H_3}C - \,C{H_3}\left( g \right)$$ at $$298 K$$ will be
A
$$-250 kJ$$
B
$$+125 kJ$$
C
$$-125 kJ$$
D
$$+250 kJ$$
Answer :
$$-125 kJ$$
290.
Consider the given diagram for $$1\,mole$$ of a gas $$X$$ and answer the following question.
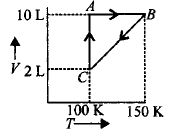
The process $$A \to B$$ represents
A
isobaric change
B
isothermal change
C
adiabatic change
D
isochoric change
Answer :
isochoric change