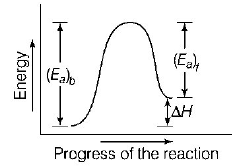
321.
From the given reactions,
$$\eqalign{
& S\left( s \right) + \frac{3}{2}{O_2}\left( g \right) \to S{O_3}\left( g \right) + 2x\,kcal \cr
& S{O_2}\left( g \right) + \frac{1}{2}{O_2}\left( g \right) \to S{O_3}\left( g \right) + y\,kcal, \cr} $$
the heat of formation of $$S{O_2}$$ is
A
$$\left( {x + y} \right)$$
B
$$\left( {x - y} \right)$$
C
$$\left( {2x + y} \right)$$
D
$$\left( {2x - y} \right)$$
Answer :
$$\left( {2x - y} \right)$$
322.
For a reaction : $${C_{\left( s \right)}} + {O_{2\left( g \right)}} \to C{O_{2\left( g \right)}}$$
What is the relation between enthalpy of reaction $$\left( {\Delta {H_r}} \right),$$ enthalpy of formation of $$C{O_2}\left( {\Delta {H_f}} \right)$$ and enthalpy of combustion of carbon $$\left( {\Delta {H_{{\text{comb}}}}} \right)?$$
A
$$\Delta {H_r} > \Delta {H_f} = \Delta {H_{{\text{comb}}}}$$
B
$$\Delta {H_r} = \Delta {H_f} = \Delta {H_{{\text{comb}}}}$$
C
$$\Delta {H_r} = \Delta {H_f} + \Delta {H_{{\text{comb}}}}$$
D
$$\Delta {H_r} = 2 \times \Delta {H_f}$$
Answer :
$$\Delta {H_r} = \Delta {H_f} = \Delta {H_{{\text{comb}}}}$$
323. A reaction having equal energies of activation for forward and reverse reactions has
A
$$\Delta S = 0$$
B
$$\Delta G = 0$$
C
$$\Delta H = 0$$
D
$$\Delta H = \Delta G = \Delta S = 0$$
Answer :
$$\Delta H = 0$$
324. The standard enthalpy of formation $$\left( {{\Delta _f}{H^ \circ }} \right)$$ at $$298 K$$ for methane, $$C{H_4}\left( g \right)$$ is $$ - 74.8\,kJ\,mo{l^{ - 1}}.$$ The additional information required to determine the average energy for $$C - H$$ bond formation would be
A
the first four ionization energies of carbon and electron gain enthalpy of hydrogen
B
the dissociation energy of hydrogen molecule, $${H_2}$$
C
the dissociation energy of $${H_2}$$ and enthalpy of sublimation of carbon
D
latent heat of vapourization of methane
Answer :
the dissociation energy of $${H_2}$$ and enthalpy of sublimation of carbon
325. If $$w$$ is the amount of work done by the system and $$q$$ is the amount of heat supplied to the system, identify the type of the system.
A
Isolated system
B
Closed system
C
Open system
D
System with thermally conducting walls
Answer :
Closed system
326. Identify the correct statement for change of Gibbs free energy for a system $$\left( {\Delta {G_{{\text{system}}}}} \right)$$ at constant temperature and pressure.
A
If $$\Delta {G_{{\text{system}}}} > 0,$$ the process is spontaneous
B
If $$\Delta {G_{{\text{system}}}} = 0,$$ the system has attained equilibrium
C
If $$\Delta {G_{{\text{system}}}} = 0,$$ the system is still moving in a particular direction
D
If $$\Delta {G_{{\text{system}}}} < 0,$$ the process is not spontaneous
Answer :
If $$\Delta {G_{{\text{system}}}} = 0,$$ the system has attained equilibrium
327. Consider the reaction : $${N_2} + 3{H_2} \to 2N{H_3}$$ carried out at constant temperature and pressure. If $$\Delta H\,{\text{and}}\,\Delta U$$ are the enthalpy and internal energy changes for the reaction, which of the following expressions is true ?
A
$$\Delta H > \Delta U$$
B
$$\Delta H < \Delta U$$
C
$$\Delta H = \Delta U$$
D
$$\Delta H = 0$$
Answer :
$$\Delta H < \Delta U$$
328. Which one of the following is correct option for free expansion of an ideal gas under adiabatic condition?
A
$$q \ne 0,\,\,\Delta T = 0,\,\,W = 0$$
B
$$q = 0,\,\,\Delta T = 0,\,\,W = 0$$
C
$$q = 0,\,\,\Delta T < 0,\,\,W \ne 0$$
D
$$q = 0,\,\,\Delta T \ne 0,\,\,W = 0$$
Answer :
$$q = 0,\,\,\Delta T = 0,\,\,W = 0$$
329.
$$\eqalign{
& Pb{O_2} \to PbO,\,\Delta {G_{298}} < 0 \cr
& Sn{O_2} \to SnO,\,\Delta {G_{298}} > 0 \cr} $$
Most probable oxidation state of $$Pb$$ and $$Sn$$ will be
A
$$P{b^{4 + }},S{n^{4 + }}$$
B
$$P{b^{4 + }},S{n^{2 + }}$$
C
$$P{b^{2 + }},\,S{n^{2 + }}$$
D
$$P{b^{2 + }},S{n^{4 + }}$$
Answer :
$$P{b^{2 + }},S{n^{4 + }}$$