181. The limiting position of the point of intersection of the lines $$3x+4y=1$$ and $$\left( {1 + c} \right)x + 3{c^2}y = 2$$ as $$c$$ tends to 1 is :
A
$$\left( { - 5,\,4} \right)$$
B
$$\left( {5,\, - 4} \right)$$
C
$$\left( {4,\, - 5} \right)$$
D
none of these
Answer :
$$\left( { - 5,\,4} \right)$$
182. The parametric equation of a line is given by $$x = - 2 + \frac{r}{{\sqrt {10} }}$$ and $$y = 1 + 3\frac{r}{{\sqrt {10} }}.$$ Then, for the line :
A
intercept on the $$x$$-axis $$ = \frac{7}{3}$$
B
intercept on the $$y$$-axis $$ = - 7$$
C
slope of the line $$ = {\tan ^{ - 1}}\frac{1}{3}$$
D
slope of the line $$ = {\tan ^{ - 1}}3$$
Answer :
slope of the line $$ = {\tan ^{ - 1}}3$$
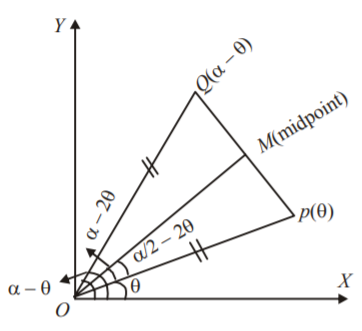
183. Let $$0 < \alpha < \frac{\pi }{2}$$ be a fixed angle. If $$P\left( {\cos \,\theta ,\,\sin \,\theta } \right)$$ and $$Q\left( {\cos \left( {\alpha - \theta } \right),\,\sin \left( {\alpha - \theta } \right)} \right),$$ then $$Q$$ is obtained from $$P$$ by the :
A
clockwise rotation around the origin through an angle $$\alpha $$
B
anticlockwise rotation around the origin through an angle $$\alpha $$
C
reflection in the line through the origin with slope $$\tan \,\alpha $$
D
reflection in the line through the origin with slope $$\tan \left( {\frac{\alpha }{2}} \right)$$
Answer :
reflection in the line through the origin with slope $$\tan \left( {\frac{\alpha }{2}} \right)$$
184. The equation of straight line passing through $$\left( { - a,\,0} \right)$$ and making a triangle with the axes of area $$T$$ is :
A
$$2Tx + {a^2}y + 2aT = 0$$
B
$$2Tx - {a^2}y + 2aT = 0$$
C
$$2Tx - {a^2}y - 2aT = 0$$
D
None of these
Answer :
$$2Tx - {a^2}y + 2aT = 0$$
185. What is the acute angle between the lines represented by the equations $$y - \sqrt 3 x - 5 = 0$$ and $$\sqrt 3 y - x + 6 = 0\,?$$
A
$${30^ \circ }$$
B
$${45^ \circ }$$
C
$${60^ \circ }$$
D
$${75^ \circ }$$
Answer :
$${30^ \circ }$$
186. The graph of the function $$\cos \,x.\cos \left( {x + 2} \right) - {\cos ^2}\left( {x + 1} \right)\,$$ is a :
A
straight line passing through the point $$\left( {0,\, - {{\sin }^2}1} \right)$$ with slope 2
B
straight line passing through the origin
C
parabola with vertex $$\left( {1,\, - {{\sin }^2}1} \right)$$
D
straight line passing through the point $$\left( {\frac{\pi }{2},{\mkern 1mu} - {{\sin }^2}1} \right)$$ and parallel to the $$x$$-axis
Answer :
straight line passing through the point $$\left( {\frac{\pi }{2},{\mkern 1mu} - {{\sin }^2}1} \right)$$ and parallel to the $$x$$-axis
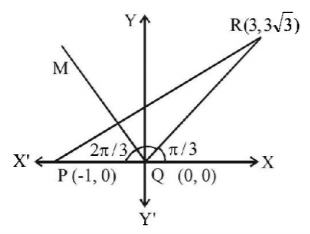
187. Let $$P = \,\left( { - 1,\,0} \right),\,Q = \left( {0,\,0} \right)$$ and $$R = \left( {3,\,3\sqrt 3 } \right)$$ be three point. The equation of the bisector of the angle $$PQR$$ is-
A
$$\frac{{\sqrt 3 }}{2}x + y = 0$$
B
$$x + \sqrt {3y} = 0$$
C
$$\sqrt 3 x + y = 0$$
D
$$x + \frac{{\sqrt 3 }}{2}y = 0$$
Answer :
$$\sqrt 3 x + y = 0$$