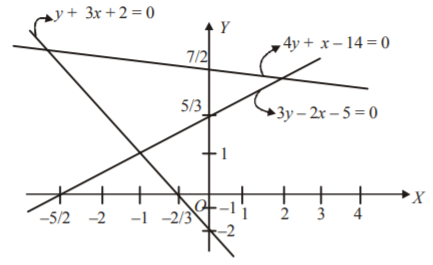
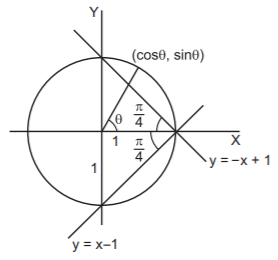21. The range of value of $$\alpha $$ such that $$\left( {0,\,\alpha } \right)$$ lies on or inside the triangle formed by the lines $$y + 3x + 2 = 0,\,3y - 2x - 5 = 0,\,4y + x - 14 = 0\,{\text{is :}}$$
A
$${\text{5 < }}\alpha \leqslant 7$$
B
$$\frac{1}{2} \leqslant \alpha \leqslant 1$$
C
$$\frac{5}{3} \leqslant \alpha \leqslant \frac{7}{2}$$
D
None of these
Answer :
$$\frac{5}{3} \leqslant \alpha \leqslant \frac{7}{2}$$
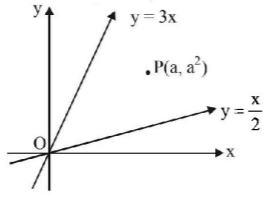
22. If $$\left( {a,\,{a^2}} \right)$$ falls inside the angle made by the lines $$y = \frac{x}{2},\,x > 0$$ and $$y = 3x,\,x > 0$$ then $$a$$ belong to-
A
$$\left( {0,\,\frac{1}{2}} \right)$$
B
$$\left( {3,\,\infty } \right)$$
C
$$\left( {\frac{1}{2},\,3} \right)$$
D
$$\left( { - 3,\, - \frac{1}{2}} \right)$$
Answer :
$$\left( {\frac{1}{2},\,3} \right)$$
23. The equation of the bisector of the acute angle between the lines $$2x-y+4=0$$ and $$x-2y=1$$ is :
A
$$x+y+5=0$$
B
$$x-y+1=0$$
C
$$x-y=5$$
D
none of these
Answer :
$$x-y+1=0$$
24. If $$\left( { - 4,\,5} \right)$$ is one vertex and $$7x - y + 8 = 0$$ is one diagonal of a square, then the equation of second diagonal is :
A
$$x + 3y = 21$$
B
$$2x - 3y = 7$$
C
$$x + 7y = 31$$
D
$$2x + 3y = 21$$
Answer :
$$x + 7y = 31$$
25. If the point $$P\left( {x,\,y} \right)$$ is equidistant from the points $$A\left( {a + b,\,b - a} \right)$$ and $$B\left( {a - b,\,a + b} \right)$$ then :
A
$$ax = by$$
B
$$bx = ay{\text{ and }}P{\text{ can be }}\left( {a,\,b} \right)$$
C
$${x^2} - {y^2} = 2\left( {ax + by} \right)$$
D
None of the above
Answer :
$$bx = ay{\text{ and }}P{\text{ can be }}\left( {a,\,b} \right)$$
26. The centroid of the triangle whose three sides are given by the combined equation $$\left( {{x^2} + 7xy + 2{y^2}} \right)\left( {y - 1} \right) = 0$$ is :
A
$$\left( {\frac{2}{3},\,0} \right)$$
B
$$\left( {\frac{7}{3},\,\frac{2}{3}} \right)$$
C
$$\left( { - \frac{7}{3},\,\frac{2}{3}} \right)$$
D
none of these
Answer :
$$\left( { - \frac{7}{3},\,\frac{2}{3}} \right)$$
27. The orthocenter of the triangle formed by the lines $$xy = 0$$ and $$x+y=1$$ is-
A
$$\left( {\frac{1}{2},\,\frac{1}{2}} \right)$$
B
$$\left( {\frac{1}{3},\,\frac{1}{3}} \right)$$
C
$$\left( {0,\,0} \right)$$
D
$$\left( {\frac{1}{4},\,\frac{1}{4}} \right)$$
Answer :
$$\left( {0,\,0} \right)$$
28. The points $$\left( {\alpha ,\,\beta ,} \right),\,\left( {\gamma ,\,\delta } \right),\,\left( {\alpha ,\,\delta } \right)$$ and $$\left( {\gamma ,\,\beta } \right)$$ taken in order, where $$\alpha ,\,\beta ,\,\gamma ,\,\delta $$ are different real numbers, are :
A
collinear
B
vertices of a square
C
vertices of a rhombus
D
concyclic
Answer :
concyclic
29. If the point $$\left( {\cos \,\theta ,\,\sin \,\theta } \right)$$ does not fall in that angle between the lines $$y = \left| {x - 1} \right|$$ in which the origin lies then $$\theta $$ belongs to :
A
$$\left( {\frac{\pi }{2},\,\frac{{3\pi }}{2}} \right)$$
B
$$\left( { - \frac{\pi }{2},\,\frac{\pi }{2}} \right)$$
C
$$\left( {0,\,\pi } \right)$$
D
none of these
Answer :
$$\left( { - \frac{\pi }{2},\,\frac{\pi }{2}} \right)$$
30. The circumradius of the triangle formed by the three lines $$y + 3x - 5 = 0 ;\,y = x$$ and $$3y - x + 10 = 0$$ is :
A
$$\frac{{25}}{{4\sqrt 2 }}$$
B
$$\frac{{25}}{{3\sqrt 2 }}$$
C
$$\frac{{25}}{{2\sqrt 2 }}$$
D
$$\frac{{25}}{{\sqrt 2 }}$$
Answer :
$$\frac{{25}}{{4\sqrt 2 }}$$