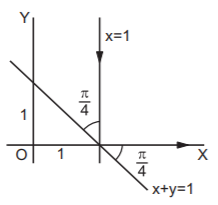61.
A rectangle $$ABCD,$$ where $$A\left( {0,\,0} \right),\,B\left( {4,\,0} \right),\,C\left( {4,\,2} \right),\,D\left( {0,\,2} \right),$$ undergoes the following transformations successively :
$$\eqalign{
& {\text{i}}{\text{.}}\,{f_1}\left( {x,\,y} \right) \to \left( {y,\,x} \right) \cr
& {\text{ii}}{\text{.}}\,{f_2}\left( {x,\,y} \right) \to \left( {x + 3y,\,y} \right) \cr
& {\text{iii}}{\text{.}}\,{f_3}\left( {x,\,y} \right) \to \left( {\frac{{\left( {x - y} \right)}}{2},\frac{{\left( {x + y} \right)}}{2}} \right) \cr} $$
The final figure will be :
A
a square
B
a rhombus
C
a rectangle
D
a parallelogram
Answer :
a parallelogram
62. If a ray travelling along the line $$x=1$$ gets reflected from the line $$x+y=1$$ then the equation of the line along which the reflected ray travels is :
A
$$y=0$$
B
$$x-y=1$$
C
$$x=0$$
D
none of these
Answer :
$$y=0$$
63. A triangle with vertices $$\left( {4,\,0} \right),\,\left( { - 1,\, - 1} \right),\,\left( {3,\,5} \right)$$ is-
A
isosceles and right angled
B
isosceles but not right angled
C
right angled but not isosceles
D
neither right angled nor isosceles
Answer :
isosceles and right angled
64. A straight line $$L$$ with negative slope passes through the point $$\left( {8,\,2} \right)$$ and cuts the positive coordinate axes at points $$P$$ and $$Q.$$ As $$L$$ varies the absolute minimum value of $$OP + OQ$$ is ($$O$$ is origin)
A
28
B
15
C
18
D
10
Answer :
18
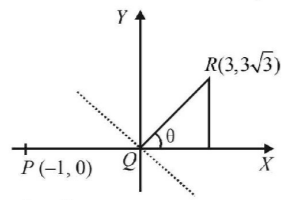
65. Let $$P = \left( { - 1,\,0} \right),\,Q = \left( {0,\,0} \right)$$ and $$R = \left( {3,\,3\sqrt 3 } \right)$$ be three points. Then the equation of the bisector of the angle $$PQR$$ is-
A
$$\frac{{\sqrt 3 }}{2}x + y = 0$$
B
$$x + \sqrt 3 y = 0$$
C
$$\sqrt 3 x + y = 0$$
D
$$x + \frac{{\sqrt 3 }}{2}y = 0$$
Answer :
$$\sqrt 3 x + y = 0$$
66. The points $$\left( { - a, - b} \right),\left( {0,\,0} \right),\left( {a,\,b} \right)$$ and $$\left( {{a^2},\,ab} \right)$$ are :
A
Collinear
B
Vertices of a parallelogram
C
Vertices of a rectangle
D
None of these
Answer :
Collinear
67. A line passing through the point $$\left( {2,\,2} \right)$$ and the axes enclose an area $$\lambda .$$ The intercepts on the axes made by the line are given by the two roots of :
A
$${x^2} - 2\left| \lambda \right|x + \left| \lambda \right| = 0$$
B
$${x^2} + \left| \lambda \right|x + 2\left| \lambda \right| = 0$$
C
$${x^2} - \left| \lambda \right|x + 2\left| \lambda \right| = 0$$
D
none of these
Answer :
$${x^2} - \left| \lambda \right|x + 2\left| \lambda \right| = 0$$
68. The orthocenter of the triangle formed by the pair of lines $$2{x^2} - xy - {y^2} + x + 2y - 1 = 0$$ and the line $$x+y+1=0$$ is :
A
$$\left( { - 1,\,0} \right)$$
B
$$\left( {0,\,1} \right)$$
C
$$\left( { - 1,\,1} \right)$$
D
none of these
Answer :
$$\left( { - 1,\,0} \right)$$
69. Given a family of lines $$a\left( {2x + y + 4} \right) + b\left( {x - 2y - 3} \right) = 0,$$ the number of lines belonging to the family at a distance $$\sqrt {10} $$ from $$P\left( {2,\, - 3} \right)$$ is :
A
$$0$$
B
$$1$$
C
$$2$$
D
$$4$$
Answer :
$$1$$
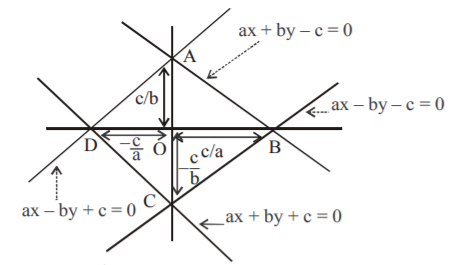
70. The area of the figure formed by the lines $$ax + by + c = 0,\,ax - by + c = 0,\,ax + by - c = 0$$ and $$ax - by - c = 0$$ is :
A
$$\frac{{{c^2}}}{{ab}}$$
B
$$\frac{{2{c^2}}}{{ab}}$$
C
$$\frac{{{c^2}}}{{2ab}}$$
D
$$\frac{{{c^2}}}{{4ab}}$$
Answer :
$$\frac{{2{c^2}}}{{ab}}$$