111. An engine is hauling a train of mass $$M\,kg$$ on a level track at a constant speed $$v\,m/s.$$ The resistance due to friction is $$f\,N/kg.$$ What extra power must the engine develop to maintain the speed up a gradient of $$h$$ in $$s$$ :
A
$$\frac{{Mghv}}{s}$$
B
$$\frac{{Mghs}}{v}$$
C
$$Mghvs$$
D
zero
Answer :
$$\frac{{Mghv}}{s}$$
112. A spring of spring constant $$5 \times {10^3}N/m$$ is stretched initially by $$5 \,cm$$ from the unstretched position. Then the work required to stretch it further by another $$5 \,cm$$ is-
A
$$12.50 \,N-m$$
B
$$18.75 \,N-m$$
C
$$25.00 \,N-m$$
D
$$6.25 \,N-m$$
Answer :
$$18.75 \,N-m$$
113.
The block of mass $$M$$ moving on the frictionless horizontal surface collides with the spring of spring constant $$k$$ and compresses it by length $$L.$$ The maximum momentum of the block after collision is-
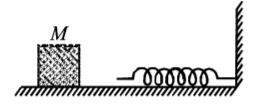
A
$$\frac{{k{L^2}}}{{2M}}$$
B
$$\sqrt {Mk} L$$
C
$$\frac{{M{L^2}}}{k}$$
D
$$Zero$$
Answer :
$$\sqrt {Mk} L$$
114. Two similar springs $$P$$ and $$Q$$ have spring constants $${K_P}$$ and $${K_Q},$$ such that $${K_P} > {K_Q}.$$ They are stretched, first by the same amount (case $$a$$), then by the same force (case $$b$$). The work done by the springs $${W_P}$$ and $${W_Q}$$ are related as, in case $$\left( a \right)$$ and case $$\left( b \right),$$ respectively
A
$${W_P} = {W_Q};{W_P} > {W_Q}$$
B
$${W_P} = {W_Q};{W_P} = {W_Q}$$
C
$${W_P} > {W_Q};{W_Q} > {W_P}$$
D
$${W_P} < {W_Q};{W_Q} < {W_P}$$
Answer :
$${W_P} > {W_Q};{W_Q} > {W_P}$$
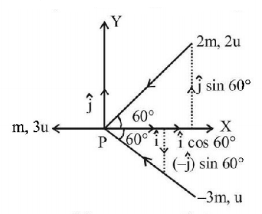
115.
Three masses $$m,2m$$ and $$3m$$ are moving in $$x-y$$ plane with speed $$3u,2u$$ and $$u$$ respectively as shown in figure. The three masses collide at the same point at $$P$$ and stick together. The velocity of resulting mass will be
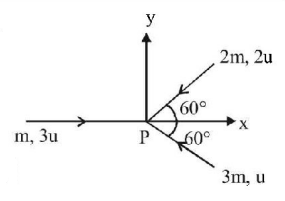
A
$$\frac{u}{{12}}\left( {\hat i + \sqrt 3 \hat j} \right)$$
B
$$\frac{u}{{12}}\left( {\hat i - \sqrt 3 \hat j} \right)$$
C
$$\frac{u}{{12}}\left( { - \hat i + \sqrt 3 \hat j} \right)$$
D
$$\frac{u}{{12}}\left( { - \hat i - \sqrt 3 \hat j} \right)$$
Answer :
$$\frac{u}{{12}}\left( { - \hat i - \sqrt 3 \hat j} \right)$$
116. A car of weight $$W$$ is on an inclined road that rises by $$100\,m$$ over a distance of $$1\,Km$$ and applies a constant frictional force $$\frac{W}{{20}}$$ on the car. While moving uphill on the road at a speed of $$10\,m{s^{ - 1}},$$ the car needs power $$P.$$ If it needs power $$\frac{P}{2}$$ while moving downhill at speed $$v$$ then value of $$v$$ is:
A
$$20\,m{s^{ - 1}}$$
B
$$5\,m{s^{ - 1}}$$
C
$$15\,m{s^{ - 1}}$$
D
$$10\,m{s^{ - 1}}$$
Answer :
$$15\,m{s^{ - 1}}$$
117. The $$KE$$ acquired by a mass $$m$$ in travelling a certain distance $$d,$$ starting from rest, under the action of a constant force is directly proportional to
A
$$m$$
B
$$\sqrt m $$
C
$$\frac{1}{{\sqrt m }}$$
D
Independent of $$m$$
Answer :
Independent of $$m$$
118. A running man has half the kinetic energy of that of a boy of half of his mass. The man speeds up by $$1\,m/s$$ so as to have same $$K.E.$$ as that of the boy. The original speed of the man will be
A
$$\sqrt 2 \,m/s$$
B
$$\left( {\sqrt 2 - 1} \right)m/s$$
C
$$\frac{1}{{\left( {\sqrt 2 - 1} \right)}}m/s$$
D
$$\frac{1}{{\sqrt 2 }}m/s$$
Answer :
$$\frac{1}{{\left( {\sqrt 2 - 1} \right)}}m/s$$
119.
If $${W_1},$$ $${W_2}$$ and $${W_3}$$ represent the work done in moving a particle from $$A$$ to $$B$$ along three different paths $$1,2$$ and $$3$$ respectively (as shown) in the gravitational field of a point mass $$m,$$ find the correct relation between $${W_1},$$ $${W_2}$$ and $${W_3}-$$
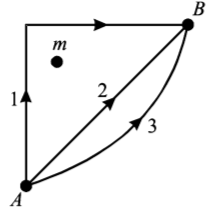
A
$${W_1} > {W_2} > {W_3}$$
B
$${W_1} = {W_2} = {W_3}$$
C
$${W_1} < {W_2} < {W_3}$$
D
$${W_2} > {W_1} > {W_3}$$
Answer :
$${W_1} = {W_2} = {W_3}$$
120.
A uniform rope of linear mass density $$\lambda $$ and length $$\ell $$ is coiled on a smooth horizontal surface. One end is pulled up with constant velocity $$v.$$ Then the average power applied by the external agent in pulling the entire rope just off the horizontal surface is
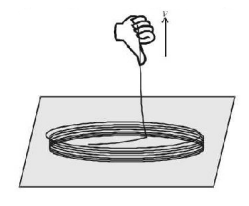
A
$$\frac{1}{2}\lambda \ell {v^2} + \frac{{\lambda {\ell ^2}g}}{2}$$
B
$$\lambda \ell gv$$
C
$$\frac{1}{2}\lambda {v^3} + \frac{{\lambda \ell vg}}{2}$$
D
$$\lambda \ell vg + \frac{1}{2}\lambda {v^3}$$
Answer :
$$\frac{1}{2}\lambda {v^3} + \frac{{\lambda \ell vg}}{2}$$