131. Calculate the $$K.E$$ and $$P.E.$$ of the ball half way up, when a ball of mass $$0.1\,kg$$ is thrown vertically upwards with an initial speed of $$20\,m{s^{ - 1}}.$$
A
$$10\,J,20\,J$$
B
$$10\,J,10\,J$$
C
$$15\,J,8\,J$$
D
$$8\,J,16\,J$$
Answer :
$$10\,J,10\,J$$
132.
A block lying on a smooth surface with spring connected to it is pulled by an external force as shown. Initially the velocity of ends $$A$$ and $$B$$ of the spring are $$4\,m/s$$ and $$2\,m/s$$ respectively. If the energy of the spring is increasing at the rate of $$20\,J/sec,$$ then the stretch in the spring is
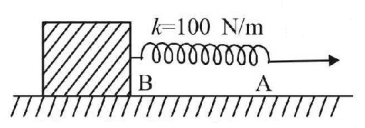
A
$$1.0\,cm$$
B
$$2.0\,cm$$
C
$$10\,cm$$
D
$$2.0\,cm$$
Answer :
$$10\,cm$$
133.
Two small bodies of masses $$'m'$$ and $$'2m'$$ are placed in a fixed smooth horizontal circular hollow tube of mean radius $$'r'$$ as shown. The mass $$'m'$$ is moving with speed $$'u'$$ and the mass $$'2\,m'$$ is stationary. After their first collision, the time elapsed for next collision is [ coefficient of restitution $$e = \frac{1}{2}$$ ]
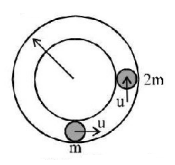
A
$$\frac{{2\pi r}}{u}$$
B
$$\frac{{4\pi r}}{u}$$
C
$$\frac{{3\pi r}}{u}$$
D
$$\frac{{12\pi r}}{u}$$
Answer :
$$\frac{{4\pi r}}{u}$$
134. A wind-powered generator converts wind energy into electrical energy. Assume that the generator converts a fixed fraction of the wind energy intercepted by its blades into electrical energy. For wind speed $$v,$$ the electrical power output will be proportional to
A
$$v$$
B
$${v^2}$$
C
$${v^3}$$
D
$${v^4}$$
Answer :
$${v^3}$$
135. Consider a drop of rain water having mass $$1\,g$$ falling from a height of $$1\,km.$$ It hits the ground with a speed of $$50\,m/s.$$ Take $$g$$ constant with a value of $$10\,m/{s^2}.$$ The work done by the (i) gravitational force and the (ii) resistive force of air is
A
$$\left( {\text{i}} \right) - 10\,J,\left( {{\text{ii}}} \right) - 8.25\,J$$
B
$$\left( {\text{i}} \right)1.25\,J,\left( {{\text{ii}}} \right) - 8.25\,J$$
C
$$\left( {\text{i}} \right)100\,J,\left( {{\text{ii}}} \right)8.75\,J$$
D
$$\left( {\text{i}} \right)10\,J,\left( {{\text{ii}}} \right) - 8.75\,J$$
Answer :
$$\left( {\text{i}} \right)10\,J,\left( {{\text{ii}}} \right) - 8.75\,J$$
136.
A $$10$$ H.P. motor pumps out water from a well of depth $$20\,m$$ and fills a water tank of volume $$22380$$ litres at a height of $$10\,m$$ from the ground. The running time of the motor to fill the empty water tank is
$$\left( {g = 10\,m{s^{ - 2}}} \right)$$
A
5 minutes
B
10 minutes
C
15 minutes
D
20 minutes
Answer :
15 minutes
137.
A force $$F$$ acting on an object varies with distance $$x$$ as shown here. The force is in newton and $$x$$ is in metre. The work done by the force in moving the object from $$x = 0$$ to $$x = 6\,m$$ is
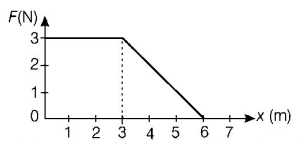
A
$$4.5\,J$$
B
$$13.5\,J$$
C
$$9.0\,J$$
D
$$18.0\,J$$
Answer :
$$13.5\,J$$
138. A uniform force of $$\left( {3\hat i + \hat j} \right)$$ newton acts on a particle of mass $$2\,kg.$$ The particle is displaced from position $$\left( {2\hat i + \hat k} \right)$$ meter to position $$\left( {4\hat i + 3\hat j - \hat k} \right)$$ meter. The work done by the force on the particle is
A
$$6\,J$$
B
$$13\,J$$
C
$$15\,J$$
D
$$9\,J$$
Answer :
$$9\,J$$
139. A block of mass $$M$$ is attached to the lower end of a vertical spring. The spring is hung from a ceiling and has force constant value $$k.$$ The mass is released from rest with the spring initially unstretched. The maximum extension produced in the length of the spring will be
A
$$\frac{{Mg}}{k}$$
B
$$\frac{{2Mg}}{k}$$
C
$$\frac{{4Mg}}{k}$$
D
$$\frac{{Mg}}{{2k}}$$
Answer :
$$\frac{{2Mg}}{k}$$
140. Two masses $$1\,g$$ and $$9\,g$$ are moving with equal kinetic energies. The ratio of the magnitudes of their respective linear momenta is
A
$$1:9$$
B
$$9:1$$
C
$$1:3$$
D
$$3:1$$
Answer :
$$1:3$$