171.
The potential energy of a $$1\,kg$$ particle free to move along the $$x-$$axis is given by $$V\left( x \right) = \left( {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right)J.$$
The total mechanical energy of the particle is $$2 \,J.$$ Then, the maximum speed (in m/s) is-
A
$$\frac{3}{{\sqrt 2 }}$$
B
$$\sqrt 2 $$
C
$$\frac{1}{{\sqrt 2 }}$$
D
$$2$$
Answer :
$$\frac{3}{{\sqrt 2 }}$$
172. An engine pumps water continuously through a hose. Water leaves the hose with a velocity $$v$$ and $$m$$ is the mass per unit length of the water jet. What is the rate at which kinetic energy is imparted to water?
A
$$\frac{1}{2}m{v^3}$$
B
$$m{v^3}$$
C
$$\frac{1}{2}m{v^2}$$
D
$$\frac{1}{2}{m^2}{v^2}$$
Answer :
$$\frac{1}{2}m{v^3}$$
173. A particle, which is constrained to move along the $$x$$-axis, is subjected to a force in the same direction which varies with the distance $$x$$ of the particle from the origin as $$F\left( x \right) = - kx + a{x^3}.$$ Here $$k$$ and $$a$$ are positive constants. For $$x \geqslant 0,$$ the functional form of the potential energy $$U\left( x \right)$$ of the particle is
A
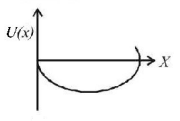

B
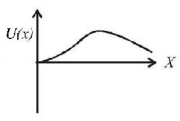

C
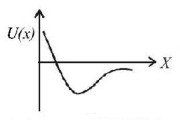

D
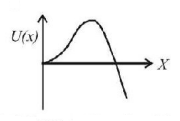

Answer :


174. $$300\,J$$ of work is done in sliding a $$2\,kg$$ block up an inclined plane of height $$10\,m.$$ Taking $$g = 10\,m/{s^2},$$ work done against friction is
A
$$100\,J$$
B
zero
C
$$1000\,J$$
D
$$200\,J$$
Answer :
$$100\,J$$
175. When a rubber-band is stretched by a distance $$x,$$ it exerts restoring force of magnitude $$F = ax + b{x^2}$$ where $$a$$ and $$b$$ are constants. The work done in stretching the unstretched rubber-band by $$L$$ is:
A
$$a{L^2} + b{L^3}$$
B
$$\frac{1}{2}\left( {a{L^2} + b{L^3}} \right)$$
C
$$\frac{{a{L^2}}}{2} + \frac{{b{L^3}}}{3}$$
D
$$\frac{1}{2}\left( {\frac{{a{L^2}}}{2} + \frac{{b{L^3}}}{3}} \right)$$
Answer :
$$\frac{{a{L^2}}}{2} + \frac{{b{L^3}}}{3}$$
176. Two bodies of masses $$4\,kg$$ and $$5\,kg$$ are moving with equal momentum. Then the ratio of their respective kinetic energies is
A
$$4:5$$
B
$$2:1$$
C
$$1:3$$
D
$$5:4$$
Answer :
$$5:4$$
177. Two identical balls $$A$$ and $$B$$ having velocities of $$0.5\,m/s$$ and $$-0.3\,m/s$$ respectively collide elastically in one dimension. The velocities of $$B$$ and $$A$$ after the collision respectively will be
A
$$-0.5\,m/s$$ and $$0.3\,m/s$$
B
$$0.5\,m/s$$ and $$-0.3\,m/s$$
C
$$-0.3\,m/s$$ and $$0.5\,m/s$$
D
$$0.3\,m/s$$ and $$0.5\,m/s$$
Answer :
$$-0.3\,m/s$$ and $$0.5\,m/s$$
178. The potential energy function for the force between two atoms in a diatomic molecule is approximately given by $$U\left( x \right) = \frac{a}{{{x^{12}}}} - \frac{b}{{{x^6}}},$$ where $$a$$ and $$b$$ are constants and $$x$$ is the distance between the atoms. If the dissociation energy of the molecule is $$D = \left[ {U\left( {x - \infty } \right) - {U_{{\text{at equilibrium}}}}} \right],$$ $$D$$ is-
A
$$\frac{{{b^2}}}{{2a}}$$
B
$$\frac{{{b^2}}}{{12a}}$$
C
$$\frac{{{b^2}}}{{4a}}$$
D
$$\frac{{{b^2}}}{{6a}}$$
Answer :
$$\frac{{{b^2}}}{{4a}}$$
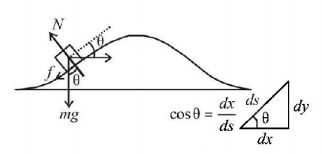
179.
A block of mass $$1\,kg$$ is pulled along the curve path $$ACB$$ by a tangential force as shown in figure. The work done by the frictional force when the block moves from $$A$$ to $$B$$ is
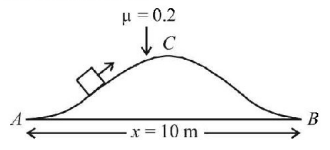
A
$$5\,J$$
B
$$10\,J$$
C
$$20\,J$$
D
None of these
Answer :
$$20\,J$$
180.
The components of a force acting on a particle are varying according to the graphs shown. When the particles move from $$\left( {0,5,6} \right)$$ to $$\left( {2,10,0} \right)$$ then the work done by this force is
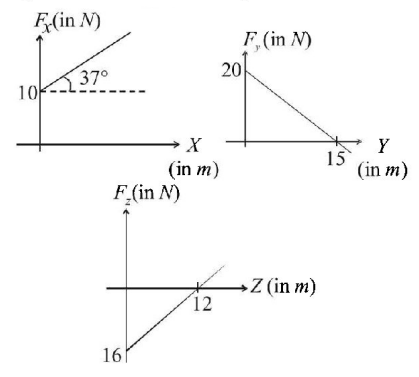
A
$$192\,J$$
B
$$\frac{{400}}{3}J$$
C
$$\frac{{287}}{2}J$$
D
None of these
Answer :
$$\frac{{287}}{2}J$$