181. The position of a particle of mass $$4\,g,$$ acted upon by a constant force is given by $$x = 4{t^2} + t,$$ where $$x$$ is in metre and $$t$$ in second. The work done during the first $$2$$ seconds is
A
$$128\,mJ$$
B
$$512\,mJ$$
C
$$576\,mJ$$
D
$$144\,mJ$$
Answer :
$$576\,mJ$$
182. A body of mass $$'m ’,$$ accelerates uniformly from rest to $$'{v_1}'$$ in time $$'{t_1}'.$$ The instantaneous power delivered to the body as a function of time $$'t '$$ is-
A
$$\frac{{m{v_1}{t^2}}}{{{t_1}}}$$
B
$$\frac{{mv_1^2t}}{{t_1^2}}$$
C
$$\frac{{m{v_1}t}}{{{t_1}}}$$
D
$$\frac{{mv_1^2t}}{{{t_1}}}$$
Answer :
$$\frac{{mv_1^2t}}{{t_1^2}}$$
183. A particle of mass $$m$$ is moving in a circular path of constant radius $$r$$ such that its centripetal acceleration $${a_c}$$ is varying with time $$t$$ as $${a_c} = {k^2}r{t^2}$$ where $$k$$ is a constant. The power delivered to the particles by the force acting on it is:
A
$$2\pi m{k^2}{r^2}t$$
B
$$m{k^2}{r^2}t$$
C
$$\frac{{\left( {m{k^4}{r^2}{t^5}} \right)}}{3}$$
D
Zero
Answer :
$$m{k^2}{r^2}t$$
184. If the momentum of a body is increased by $$50\% ,$$ then the percentage increase in its kinetic energy is
A
$$50\% $$
B
$$100\% $$
C
$$125\% $$
D
$$200\% $$
Answer :
$$125\% $$
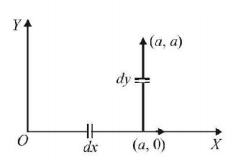
185. A force $$F = - K\left( {y\hat i + x\hat j} \right)$$ (where $$K$$ is a positive constant) acts on a particle moving in the $$xy$$ plane. Starting from the origin, the particle is taken along the positive $$x$$ axis to the point $$\left( {a,0} \right),$$ and then parallel to the $$y$$ axis to the point $$\left( {a,a} \right).$$ The total work done by the force $$F$$ on the particle is
A
$$ - 2K{a^2}$$
B
$$2K{a^2}$$
C
$$ - K{a^2}$$
D
$$K{a^2}$$
Answer :
$$ - K{a^2}$$
186. A block of mass $$0.50 \,kg$$ is moving with a speed of $$2.00\,m{s^{ - 1}}$$ on a smooth surface. It strikes another mass of $$1.00 \,kg$$ and then they move together as a single body. The energy loss during the collision is-
A
$$0.16\,J$$
B
$$1.00\,J$$
C
$$0.67\,J$$
D
$$0.34\,J$$
Answer :
$$0.67\,J$$
187. A body of mass $$1\,kg$$ begins to move under the action of a time dependent force $$\vec F = \left( {2t\hat i + 3{t^2}\hat j} \right)N,$$ where $${\hat i}$$ and $${\hat j}$$ are unit vectors along $$x$$ and $$y$$ axis. What power will be developed by the force at the time $$t$$ ?
A
$$\left( {2{t^2} + 3{t^3}} \right)W$$
B
$$\left( {2{t^2} + 4{t^4}} \right)W$$
C
$$\left( {2{t^3} + 3{t^4}} \right)W$$
D
$$\left( {2{t^3} + 3{t^5}} \right)W$$
Answer :
$$\left( {2{t^3} + 3{t^5}} \right)W$$
188.
A block of mass $$m = 0.1\,kg$$ is connected to a spring of unknown spring constant $$k.$$ It is compressed to a distance $$x$$ from its equilibrium position and released from rest. After approaching half the distance $$\left( {\frac{x}{2}} \right)$$ from equilibrium position, it hits another block and comes to rest momentarily, while the other block moves with a velocity $$3\,m{s^{ - 1}}.$$
The total initial energy of the spring is
A
$$0.3\,J$$
B
$$0.6\,J$$
C
$$0.8\,J$$
D
$$1.5\,J$$
Answer :
$$0.6\,J$$
189. A particle, which is constrained to move along the x-axis, is subjected to a force in the same direction which varies with the distance $$x$$ of the particle from the origin as $$F\left( x \right) = - kx + a{x^3}.$$ Here $$k$$ and $$a$$ are positive constants. For $$x \geqslant 0,$$ the functional form of the potential energy $$U\left( x \right)$$ of the particle is-
A
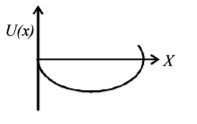

B
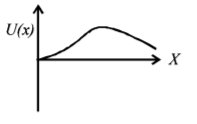

C


D
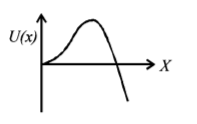

Answer :


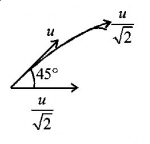
190. A ball whose kinetic energy is $$E,$$ is projected at an angle of $${45^ \circ }$$ to the horizontal. The kinetic energy of the ball at the highest point of its flight will be
A
$$E$$
B
$$\frac{E}{{\sqrt 2 }}$$
C
$$\frac{E}{2}$$
D
zero.
Answer :
$$\frac{E}{2}$$