81. An engine pumps water through a hose pipe. Water passes through the pipe and leaves it with a velocity of $$2\,m{s^{ - 1}}.$$ The mass per unit length of water in the pipe is $$100\,kg\,{m^{ - 1}}.$$ What is the power of the engine?
A
$$400\,W$$
B
$$200\,W$$
C
$$100\,W$$
D
$$800\,W$$
Answer :
$$800\,W$$
82. If two persons $$A$$ and $$B$$ take $$2$$ seconds and $$4$$ seconds respectively to lift an object to the same height $$h,$$ then the ratio of their powers is
A
$$1:2$$
B
$$1:1$$
C
$$2:1$$
D
$$1:3$$
Answer :
$$2:1$$
83. A block of mass $$10\,kg,$$ moving in $$x$$-direction with a constant speed of $$10\,m{s^{ - 1}},$$ is subjected to a retarding force $$F = 0.1\,x\,J/m$$ during its travel from $$x = 20\,m$$ to $$30\,m.$$ Its final $$KE$$ will be
A
$$475\,J$$
B
$$450\,J$$
C
$$275\,J$$
D
$$250\,J$$
Answer :
$$475\,J$$
84. A child is swinging a swing. Minimum and maximum heights of swing from the earth's surface are $$0.75\,m$$ and $$2\,m$$ respectively. The maximum velocity of this swing is
A
$$5\,m/s$$
B
$$10\,m/s$$
C
$$15\,m/s$$
D
$$20\,m/s$$
Answer :
$$5\,m/s$$
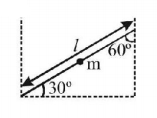
85. A rod of mass $$m$$ and length $$\ell $$ is made to stand at an angle of $${60^ \circ }$$ with the vertical. Potential energy of the rod in this position is
A
$$mg\,\ell $$
B
$$\frac{{mg\,\ell }}{2}$$
C
$$\frac{{mg\,\ell }}{3}$$
D
$$\frac{{mg\,\ell }}{4}$$
Answer :
$$\frac{{mg\,\ell }}{4}$$
86. A particle of mass $$100\,g$$ is thrown vertically upwards with a speed of $$5 \,m/s.$$ The work done by the force of gravity during the time the particle goes up is-
A
$$-0.5\,J$$
B
$$-1.25\,J$$
C
$$1.25\,J$$
D
$$0.5\,J$$
Answer :
$$-1.25\,J$$
87. A body moves a distance of $$10\,m$$ along a straight line under the action of a force of $$5$$ newtons. If the work done is $$25$$ joules, the angle which the force makes with the direction of motion of body is
A
$${0^ \circ }$$
B
$${30^ \circ }$$
C
$${60^ \circ }$$
D
$${90^ \circ }$$
Answer :
$${60^ \circ }$$
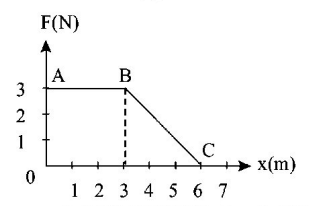
88.
A force $$F$$ acting on an object varies with distance $$x$$ as shown here. The force is in $$N$$ and $$x$$ in $$m.$$ The work done by the force in moving the object from $$x = 0$$ to $$x = 6\,m$$ is
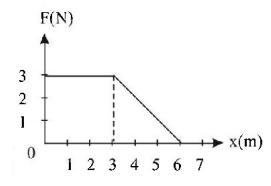
A
$$18.0\,J$$
B
$$13.5\,J$$
C
$$9.0\,J$$
D
$$4.5\,J$$
Answer :
$$13.5\,J$$
89. A metal ball of mass $$2\,kg$$ moving with a velocity of $$36\,km/h$$ has a head on collision with a stationary ball of mass $$3\,kg.$$ If after the collision, the two balls move together, the loss in kinetic energy due to collision is
A
$$140\,J$$
B
$$100\,J$$
C
$$60\,J$$
D
$$40\,J$$
Answer :
$$60\,J$$
90. A body of mass $$m$$ is accelerated uniformly from rest to a speed $$v$$ in a time $$T.$$ The instantaneous power delivered to the body as a function of time is given by-
A
$$\frac{{m{v^2}}}{{{T^2}}}.{t^2}$$
B
$$\frac{{m{v^2}}}{{{T^2}}}.t$$
C
$$\frac{1}{2}\frac{{m{v^2}}}{{{T^2}}}.{t^2}$$
D
$$\frac{1}{2}\frac{{m{v^2}}}{{{T^2}}}.t$$
Answer :
$$\frac{{m{v^2}}}{{{T^2}}}.t$$