91.
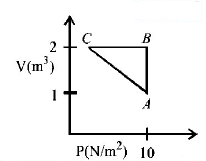
An ideal gas is taken through the cycle $$A \to B \to C \to A,$$ as shown in the figure. If the net heat supplied to the gas in the cycle is $$5\,J,$$ the work done by the gas in the process $$C → A$$ is
A
$$ - 5 \,J$$
B
$$ - 10\, J$$
C
$$ - 15\, J$$
D
$$ - 20\, J$$
Answer :
$$ - 5 \,J$$
92. When $$1\,kg$$ of ice at $${0^ \circ }C$$ melts to water at $${0^ \circ }C,$$ the resulting change in its entropy, taking latent heat of ice to be $$80\,cal{/^ \circ }C,$$ is
A
$$8 \times {10^4}cal/K$$
B
$$80\,cal/K$$
C
$$293\,cal/K$$
D
$$273\,cal/K$$
Answer :
$$293\,cal/K$$
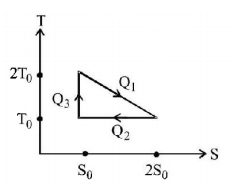
93.
The temperature-entropy diagram of a reversible engine cycle is given in the figure. Its efficiency is
A
$$\frac{1}{4}$$
B
$$\frac{1}{2}$$
C
$$\frac{2}{3}$$
D
$$\frac{1}{3}$$
Answer :
$$\frac{1}{3}$$
94. An ideal gas heat engine operates in a Carnot cycle between $${227^ \circ }C$$ and $${127^ \circ }C.$$ It absorbs $$6\,kcal$$ at the higher temperature. The amount of heat (in $$kcal$$ ) converted into work is equal to
A
1.6
B
1.2
C
4.8
D
3.5
Answer :
1.2
95.
When the state of a gas adiabatically changed from an equilibrium state $$A$$ to another equilibrium state $$B$$ an amount of work done on the stystem is $$35\,J.$$ If the gas is taken from state $$A$$ to $$B$$ via process in which the net heat absorbed by the system is $$12\,cal,$$ then the net work done by the system is
$$\left( {1\,cal = 4.19\,J} \right)$$
A
$${13.2\,J}$$
B
$${15.4\,J}$$
C
$${12.6\,J}$$
D
$${16.8\,J}$$
Answer :
$${15.4\,J}$$
96. Which of the following statements is correct for any thermodynamic system ?
A
The change in entropy can never be zero
B
Internal energy and entropy and state functions
C
The internal energy changes in all processes
D
The work done in an adiabatic process is always zero.
Answer :
Internal energy and entropy and state functions
97. In a given process on an ideal gas, $$dW = 0$$ and $$dQ < 0.$$ Then for the gas
A
the temperature will decrease
B
the volume will increase
C
the pressure will remain constant
D
the temperature will increase
Answer :
the temperature will decrease
98. If the amount of heat given to a system is $$35\,J$$ and the amount of work done on the system is $$15\,J,$$ then the change in internal energy of the system is
A
$$ - 50\,J$$
B
$$ 20\,J$$
C
$$ 30\,J$$
D
$$ 50\,J$$
Answer :
$$ 50\,J$$
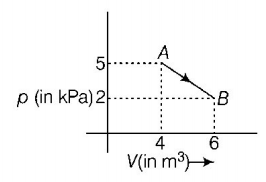
99.
One mole of an ideal diatomic gas undergoes a transition from $$A$$ to $$B$$ along a path $$AB$$ as shown in the figure.
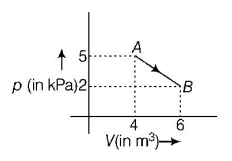
The change in internal energy of the gas during the transition is
A
$$20\,kJ$$
B
$$-20\,kJ$$
C
$$20\,J$$
D
$$-12\,kJ$$
Answer :
$$-20\,kJ$$
100.
The state of an ideal gas is changed through an isothermal process at temperature $${T_0}$$ as shown in figure. The work done by gas in going from state $$B$$ to $$C$$ is double the work done by gas in going from state $$A$$ to $$B.$$ If the pressure in the state $$B$$ is $$\frac{{{P_0}}}{2}$$ then the pressure of the gas in state $$C$$ is
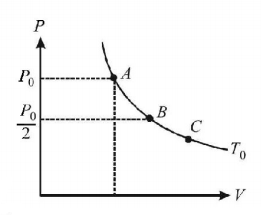
A
$$\frac{{{P_0}}}{2}$$
B
$$\frac{{{P_0}}}{4}$$
C
$$\frac{{{P_0}}}{6}$$
D
$$\frac{{{P_0}}}{8}$$
Answer :
$$\frac{{{P_0}}}{8}$$