111. A mass of diatomic gas $$\left( {\gamma = 1.4} \right)$$ at a pressure of 2 atmospheres is compressed adiabatically so that its temperature rises from $${27^ \circ }C$$ to $${927^ \circ }C.$$ The pressure of the gas in final state is
A
$$28\,atm$$
B
$$68.7\,atm$$
C
$$256\,atm$$
D
$$8\,atm$$
Answer :
$$256\,atm$$
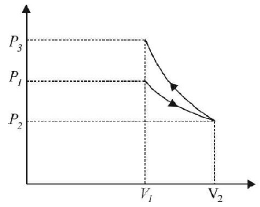
112. An ideal gas is initially at $${P_1},{V_1}$$ is expanded to $${P_2},{V_2}$$ and then compressed adiabatically to the same volume $${V_1}$$ and pressure $${P_3}.$$ If $$W$$ is the net work done by the gas in complete process which of the following is true
A
$$W > 0;{P_3} > {P_1}$$
B
$$W < 0;{P_3} > {P_1}$$
C
$$W > 0;{P_3} < {P_1}$$
D
$$W < 0;{P_3} < {P_1}$$
Answer :
$$W < 0;{P_3} > {P_1}$$
113. A Carnot engine takes $$3 \times {10^6}\,cal.$$ of heat from a reservoir at $${627^ \circ }C,$$ and gives it to a sink at $${27^ \circ }C.$$ The work done by the engine is
A
$$4.2 \times {10^6}\,J$$
B
$$8.4 \times {10^6}\,J$$
C
$$16.8 \times {10^6}\,J$$
D
zero
Answer :
$$8.4 \times {10^6}\,J$$
114. During an isothermal expansion, a confined ideal gas does $$-150\,J$$ of work against its surroundings. This implies that
A
$$150\,J$$ heat has been removed from the gas
B
$$300\,J$$ of heat has been added to the gas
C
no heat is transferred because the process is isothermal
D
$$250\,J$$ of heat has been added to the gas
Answer :
$$150\,J$$ heat has been removed from the gas
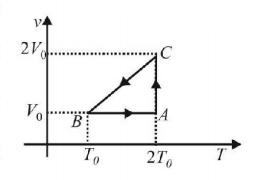
115.
The efficiency of an ideal gas with adiabatic exponent $$'\gamma '$$ for the shown cyclic process would be
A
$$\frac{{\left( {2\ln 2 - 1} \right)}}{{\frac{\gamma }{{\left( {\gamma - 1} \right)}}}}$$
B
$$\frac{{\left( {1 - 2\ln 2} \right)}}{{\frac{\gamma }{{\left( {\gamma - 1} \right)}}}}$$
C
$$\frac{{\left( {2\ln 2 + 1} \right)}}{{\frac{\gamma }{{\left( {\gamma - 1} \right)}}}}$$
D
$$\frac{{\left( {2\ln 2 - 1} \right)}}{{\frac{\gamma }{{\left( {\gamma + 1} \right)}}}}$$
Answer :
$$\frac{{\left( {2\ln 2 - 1} \right)}}{{\frac{\gamma }{{\left( {\gamma - 1} \right)}}}}$$
116. Which of the following processes is reversible?
A
Transfer of heat by radiation
B
Electrical heating of a nichrome wire
C
Transfer of heat by conduction
D
Isothermal compression
Answer :
Isothermal compression
117. The molar specific heats of an ideal gas at constant pressure and volume are denoted by $${C_p}$$ and $${C_V}$$ respectively. If $$\gamma = \frac{{{C_p}}}{{{C_V}}}$$ and $$R$$ is the universal gas constant, then $${C_V}$$ is equal to
A
$$\frac{{1 + \gamma }}{{1 - \gamma }}$$
B
$$\frac{R}{{\left( {\gamma - 1} \right)}}$$
C
$$\frac{{\left( {\gamma - 1} \right)}}{R}$$
D
$$\gamma R$$
Answer :
$$\frac{R}{{\left( {\gamma - 1} \right)}}$$
118. If one mole of a monatomic gas $$\left( {\gamma = \frac{5}{3}} \right)$$ is mixed with one mole of a diatomic gas $$\left( {\gamma = \frac{7}{5}} \right)$$ the value of $$\gamma $$ for mixture is
A
1.40
B
1.50
C
1.53
D
3.07
Answer :
1.50
119. A diatomic ideal gas is used in a Carnot engine as the working substance. If during the adiabatic expansion part of the cycle the volume of the gas increases from $$V$$ to $$32\,V,$$ the efficiency of the engine is
A
0.5
B
0.75
C
0.99
D
0.25
Answer :
0.75
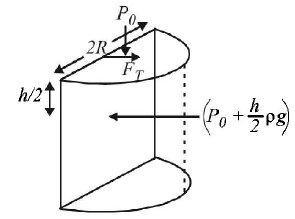
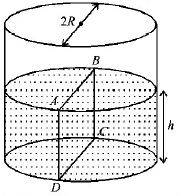
120.
Water is filled up to a height $$h$$ in a beaker of radius $$R$$ as shown in the figure. The density of water is $$\rho ,$$ the surface tension of water is $$T$$ and the atmospheric pressure is $${P_0}.$$ Consider a vertical section $$ABCD$$ of the water column through a diameter of the beaker. The force on water on one side of this section by water on the other side of this section has magnitude
A
$$\left| {2\,{P_0}Rh + \pi {R^2}\rho gh - 2\,RT} \right|$$
B
$$\left| {2\,{P_0}Rh + R\rho g{h^2} - 2\,RT} \right|$$
C
$$\left| {{P_0}\pi {R^2} + R\rho g{h^2} - 2\,RT} \right|$$
D
$$\left| {{P_0}\pi {R^2} + R\rho g{h^2} + 2\,RT} \right|$$
Answer :
$$\left| {2\,{P_0}Rh + R\rho g{h^2} - 2\,RT} \right|$$