141. During an adiabatic process of an ideal gas, if $$P$$ is proportional to $$\frac{1}{{\;{V^{1.5}}}},$$ then the ratio of specific heat capacities at constant pressure to that at constant volume for the gas is
A
1.5
B
0.25
C
0.75
D
0.4
Answer :
1.5
142.
A thermodynamic process is shown in the figure. The pressure and volumes corresponding to some points in the figure are
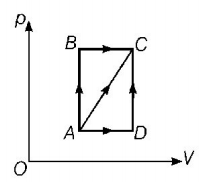
$$\eqalign{
& {p_A} = 3 \times {10^4}pa,\,\,{V_A} = 2 \times {10^{ - 3}}{m^3} \cr
& {p_B} = 8 \times {10^4}pa,\,\,{V_B} = 5 \times {10^{ - 3}}{m^3} \cr} $$
In process $$AB,600\,J$$ of heat is added to the system and in process $$BC,200\,J$$ of heat is added to the system. The change in internal energy of the system in process $$AC$$ would be
A
$$560\,J$$
B
$$800\,J$$
C
$$600\,J$$
D
$$640\,J$$
Answer :
$$560\,J$$
143. Heat given to a body which raises its temperature by $${1^ \circ }C$$ is
A
water equivalent
B
thermal capacity
C
specific heat
D
temperature gradient
Answer :
thermal capacity
144. Two moles of an ideal monoatomic gas occupies a volume $$V$$ at $${27^ \circ }C.$$ The gas expands adiabatically to a volume $$2V.$$ Calculate $$(a)$$ the final temperature of the gas and $$(b)$$ change in its internal energy.
A
(a) 189 $$K$$ (b) 2.7 $$kJ$$
B
(a) 195 $$K$$ (b) $$- 2.7 kJ$$
C
(a) 189 $$K$$ (b) $$- 2.7 kJ$$
D
(a) $$195 K$$ (b) $$2.7 kJ$$
Answer :
(a) 189 $$K$$ (b) $$- 2.7 kJ$$
145. A monatomic ideal gas, initially at temperature $${{T_1}},$$ is enclosed in a cylinder fitted with a frictionless piston. The gas is allowed to expand adiabatically to a temperature $${{T_2}}$$ by releasing the piston suddenly. If $${L_1}$$ and $${L_2}$$ are the length of the gas column before and after expansion respectively, then $$\frac{{{T_1}}}{{{T_2}}}$$ is given by
A
$${\left( {\frac{{{L_1}}}{{{L_2}}}} \right)^{\frac{2}{3}}}$$
B
$${\frac{{{L_1}}}{{{L_2}}}}$$
C
$$\frac{{{L_2}}}{{{L_1}}}$$
D
$${\left( {\frac{{{L_2}}}{{{L_1}}}} \right)^{\frac{2}{3}}}$$
Answer :
$${\left( {\frac{{{L_2}}}{{{L_1}}}} \right)^{\frac{2}{3}}}$$
146. If $$Q,E$$ and $$W$$ denote respectively the heat added, change in internal energy and the work done in a closed cycle process, then
A
$$W = 0$$
B
$$Q = W = 0$$
C
$$E = 0$$
D
$$Q = 0$$
Answer :
$$E = 0$$
147. Three perfect gases at absolute temperatures $${T_1},$$ $${T_2}$$ and $${T_3}$$ are mixed. The masses of molecules are $${m_1},$$ $${m_2}$$ and $${m_3}$$ and the number of molecules are $${n_1},$$ $${n_2}$$ and $${n_3}$$ respectively. Assuming no loss of energy, the final temperature of the mixture is :
A
$$\frac{{{n_1}{T_1} + {n_2}{T_2} + {n_3}{T_3}}}{{{n_1} + {n_2} + {n_3}}}$$
B
$$\frac{{{n_1}T_1^2 + {n_2}T_2^2 + {n_3}T_3^2}}{{{n_1}{T_1} + {n_2}{T_2} + {n_3}{T_3}}}$$
C
$$\frac{{n_1^2T_1^2 + n_2^2T_2^2 + n_3^2T_3^2}}{{{n_1}{T_1} + {n_2}{T_2} + {n_3}{T_3}}}$$
D
$$\frac{{\left( {{T_1} + {T_2} + {T_3}} \right)}}{3}$$
Answer :
$$\frac{{{n_1}{T_1} + {n_2}{T_2} + {n_3}{T_3}}}{{{n_1} + {n_2} + {n_3}}}$$
148. The internal energy change in a system that has absorbed $$2\,kcal$$ of heat and done $$500\,J$$ of work is
A
$$8900\,J$$
B
$$6400\,J$$
C
$$5400\,J$$
D
$$7900\,J$$
Answer :
$$7900\,J$$
149. Which statement is incorrect ?
A
all reversible cycles have same efficiency
B
reversible cycle has more efficiency than an irreversible
one
C
Carnot cycle is a reversible one
D
Carnot cycle has the maximum efficiency in all cycles.
Answer :
all reversible cycles have same efficiency
150. A perfect gas goes from a state $$A$$ to another state $$B$$ by absorbing $$8 \times {10^5}J$$ of heat and doing $$6.5 \times {10^5}J$$ of external work. It is now transferred between the same two states in another process in which it absorbs $${10^5}J$$ of heat. In the second process
A
work done by gas is $${10^5}J$$
B
work done on gas is $${10^5}J$$
C
work done by gas is $$0.5 \times {10^5}J$$
D
work done on the gas is $$0.5 \times {10^5}J$$
Answer :
work done on the gas is $$0.5 \times {10^5}J$$