151.
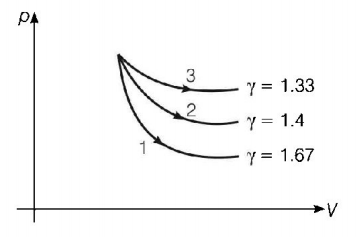
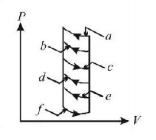
The pressure-volume diagram shows six curved paths that can be followed by the gas (connected by vertical paths). Which two of them should be part of a closed cycle if the net work done by the gas is to be its maximum positive value?
A
$$af$$
B
$$ae$$
C
$$ac$$
D
$$ce$$
Answer :
$$ae$$
152. A gas mixture consists of 2 moles of $${O_2}$$ and 4 moles of $$Ar$$ at temperature $$T.$$ Neglecting all vibrational modes, the total internal energy of the system is
A
$$4RT$$
B
$$15RT$$
C
$$9RT$$
D
$$11RT$$
Answer :
$$11RT$$
153.
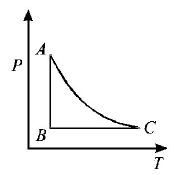
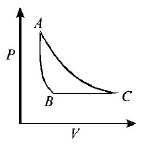
The $$PT$$ diagram for an ideal gas is shown in the figure, where $$AC$$ is an adiabatic process, find the corresponding $$PV$$ diagram.
A

B
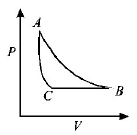

C
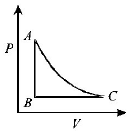

D
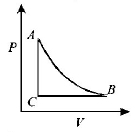

Answer :


154. An ideal gas $$A$$ and a real gas $$B$$ have their volumes increased from $$V$$ to $$2V$$ under isothermal conditions. The increase in internal energy
A
will be same in both $$A$$ and $$B$$
B
will be zero in both the gases
C
of $$B$$ will be more than that of $$A$$
D
of $$A$$ will be more than that of $$B$$
Answer :
will be zero in both the gases
155. A gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature $$T.$$ Neglecting all vibrational modes, the total internal energy of the system is
A
$$4\, RT$$
B
$$15\, RT$$
C
$$9\, RT$$
D
$$11\, RT$$
Answer :
$$11\, RT$$
156. Which of the following parameters does not characterize the thermodynamic state of matter ?
A
Temperature
B
Pressure
C
Work
D
Volume
Answer :
Work
157. One mole of an ideal gas at an initial temperature of $$TK$$ does $$6R$$ joules of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is $$\frac{5}{3},$$ the final temperature of gas will be
A
$$\left( {T + 2.4} \right)K$$
B
$$\left( {T - 2.4} \right)K$$
C
$$\left( {T + 4} \right)K$$
D
$$\left( {T - 4} \right)K$$
Answer :
$$\left( {T - 4} \right)K$$
158.
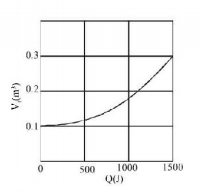
Suppose $$0.5\,mole$$ of an ideal gas undergoes an isothermal expansion as energy is added to its heat $$Q.$$
Graph shows the final volume $${V_f}$$ versus $$Q.$$ The temperature of the gas is (use $$\ln 9 = 2$$ and $$R = \frac{{25}}{3}\,J/mol - K$$ )
A
$$360\,K$$
B
$$293\,K$$
C
$$386\,K$$
D
$$412\,K$$
Answer :
$$360\,K$$
159.
An ideal gas can be expanded from an initial state to a certain volume through two different processes,
$$\left( A \right)\,P{V^2} = K$$ and $$\left( B \right)\,P = K{V^2},$$ where $$K$$ is a positive constant. Then, choose the correct option from the following.
A
Final temperature in $$\left( A \right)$$ will be greater than in $$\left( B \right)$$
B
Final temperature in $$\left( B \right)$$ will be greater than in $$\left( A \right)$$
C
Work done by the gas in both the processes would be equal
D
Total heat given to the gas in $$\left( A \right)$$ is greater than in $$\left( B \right)$$
Answer :
Final temperature in $$\left( B \right)$$ will be greater than in $$\left( A \right)$$
160.
A refrigerator works between $${4^ \circ }C$$ and $${30^ \circ }C.$$ It is required to remove 600 calories of heat every second in order to keep the temperature of the refrigerated space constant. The power required is
(Take, $$1\,cal = 4.2\,Joules$$ )
A
$$23.65\,W$$
B
$$236.5\,W$$
C
$$2365\,W$$
D
$$2.365\,W$$
Answer :
$$236.5\,W$$