171. In Carnot engine efficiency is $$40\% $$ at hot reservoir temperature $$T.$$ For efficiency $$50\% $$ what will be temperature of hot reservoir?
A
$$\frac{T}{5}$$
B
$$\frac{2T}{5}$$
C
$$6T$$
D
$$\frac{6T}{5}$$
Answer :
$$\frac{6T}{5}$$
172. Two $$kg$$ of water is converted into steam by boiling at atmospheric pressure. The volume changes from $$2 \times {10^{ - 3}}{m^3}$$ to $$3.34\,{m^3}.$$ The work done by the system is about
A
$$ - 340\,kJ$$
B
$$ - 170\,kJ$$
C
$$ 170\,kJ$$
D
$$ 340\,kJ$$
Answer :
$$ 340\,kJ$$
173. On $$P-V$$ coordinates, the slope of an isothermal curve of a gas at a pressure $$P = 1MPa$$ and volume $$V = 0.0025\,{m^3}$$ is equal to $$ - 400\,Mpa/{m^3}.$$ If $$\frac{{{C_p}}}{{{C_v}}} = 1.4,$$ the slope of the adiabatic curve passing through this point is :
A
$$ - 56\,Mpa/{m^3}$$
B
$$ - 400\,Mpa/{m^3}$$
C
$$ - 560\,Mpa/{m^3}$$
D
None of these
Answer :
$$ - 560\,Mpa/{m^3}$$
174.
In the following $$P-V$$ diagram two adiabatics cut two isothermals at temperatures $${T_1}$$ and $${T_2}$$ (fig). The value of $$\frac{{{V_a}}}{{{V_d}}}$$ will be
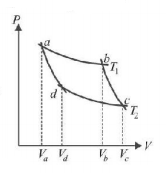
A
$$\frac{{{V_b}}}{{{V_c}}}$$
B
$$\frac{{{V_c}}}{{{V_b}}}$$
C
$$\frac{{{V_d}}}{{{V_a}}}$$
D
$${V_b}{V_c}$$
Answer :
$$\frac{{{V_b}}}{{{V_c}}}$$
175. A monatomic ideal gas, initially at temperature $${T_1},$$ is enclosed. in a cylinder fitted with a frictionless piston. The gas is allowed to expand adiabatically to a temperature $${T_2}$$ by releasing the piston suddenly. If $${L_1}$$ and $${L_2}$$ are the length of the gas column before and after expansion respectively, then $$\frac{{{T_1}}}{{{T_2}}}$$ is given by
A
$${\left( {\frac{{{L_1}}}{{{L_2}}}} \right)^{\frac{2}{3}}}$$
B
$${\frac{{{L_1}}}{{{L_2}}}}$$
C
$${\frac{{{L_2}}}{{{L_1}}}}$$
D
$${\left( {\frac{{{L_2}}}{{{L_1}}}} \right)^{\frac{2}{3}}}$$
Answer :
$${\left( {\frac{{{L_2}}}{{{L_1}}}} \right)^{\frac{2}{3}}}$$
176. Which of the following is not thermodynamical function ?
A
Enthalpy
B
Work done
C
Gibb’s energy
D
Internal energy
Answer :
Work done
177.
A solid body of constant heat capacity $$1\,J/{\,^ \circ }C$$ is being heated by keeping it in contact with reservoirs in two ways :
(i) Sequentially keeping in contact with 2 reservoirs such that each reservoir supplies same amount of heat.
(ii) Sequentially keeping in contact with 8 reservoirs such that each reservoir supplies same amount of heat.
In both the cases body is brought from initial temperature $$100°C$$ to final temperature $$200°C.$$ Entropy change of the body in the two cases respectively is:
A
$$ln\,2, 2\,ln\,2$$
B
$$2\,ln\,2, 8\,ln\,2$$
C
$$ln\,2, 4\,ln\,2$$
D
$$ln\,2, ln\,2$$
Answer :
$$ln\,2, ln\,2$$
178. The internal energy change in a system that has absorbed $$2\,Kcal$$ of heat and done $$500\,J$$ of work is
A
$$8900\,J$$
B
$$6400\,J$$
C
$$5400\,J$$
D
$$7900\,J$$
Answer :
$$7900\,J$$
179. A closed compartment containing gas is moving with some acceleration in horizontal direction. Neglect effect of gravity. Then the pressure in the compartment is
A
same everywhere
B
lower in the front side
C
lower in the rear side
D
lower in the upper side
Answer :
lower in the front side
180. 5.6 liter of helium gas at STP is adiabatically compressed to 0.7 liter. Taking the initial temperature to be $${T_1},$$ the work done in the process is
A
$$\frac{9}{8}\,R{T_1}$$
B
$$\frac{3}{2}\,R{T_1}$$
C
$$\frac{15}{8}\,R{T_1}$$
D
$$\frac{9}{2}\,R{T_1}$$
Answer :
$$\frac{9}{8}\,R{T_1}$$