31. Let $$E$$ be the ellipse $$\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1$$ and $$C$$ be the circle $${x^2} + {y^2} = 9.$$ Let $$P$$ and $$Q$$ be the points $$\left( {1,\,2} \right)$$ and $$\left( {2,\,1} \right)$$ respectively. Then-
A
$$Q$$ lies inside $$C$$ but outside $$E$$
B
$$Q$$ lies outside both $$C$$ and $$E$$
C
$$P$$ lies inside both $$C$$ and $$E$$
D
$$P$$ lies inside $$C$$ but outside $$E$$
Answer :
$$P$$ lies inside $$C$$ but outside $$E$$
32. The sum of the focal distances of a point on the ellipse $$\frac{{{x^2}}}{4} + \frac{{{y^2}}}{9} = 1$$ is :
A
$$4$$ units
B
$$6$$ units
C
$$8$$ units
D
$$10$$ units
Answer :
$$4$$ units
33. If in an ellipse the minor axis $$=$$ the distance between the foci and its latus rectum $$=$$ 10 then the equation of the ellipse in the standard form is :
A
$$\frac{{{x^2}}}{{{{\left( {10} \right)}^2}}} + \frac{{{y^2}}}{{{{\left( {5\sqrt 2 } \right)}^2}}} = 1$$
B
$$\frac{{{x^2}}}{{{{\left( {5\sqrt 2 } \right)}^2}}} + \frac{{{y^2}}}{{{{\left( {10} \right)}^2}}} = 1$$
C
$$\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{{{\left( {\frac{5}{{\sqrt 2 }}} \right)}^2}}} = 1$$
D
none of these
Answer :
$$\frac{{{x^2}}}{{{{\left( {10} \right)}^2}}} + \frac{{{y^2}}}{{{{\left( {5\sqrt 2 } \right)}^2}}} = 1$$
34. If $$p$$ is the length of the perpendicular from the focus $$S$$ of the ellipse $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$ to a tangent at a point $$P$$ on the ellipse, then $$\frac{{2a}}{{SP}} - 1 = ?$$
A
$$\frac{{{a^2}}}{{{p^2}}}$$
B
$$\frac{{{b^2}}}{{{p^2}}}$$
C
$${p^2}$$
D
$$\frac{{{a^2} + {b^2}}}{{{p^2}}}$$
Answer :
$$\frac{{{b^2}}}{{{p^2}}}$$
35. In the ellipse $${x^2} + 3{y^2} = 9$$ the distance between the foci is :
A
$$\sqrt 6 $$
B
$$3$$
C
$$\frac{2}{3}\sqrt 6 $$
D
$$2\sqrt 6 $$
Answer :
$$2\sqrt 6 $$
36. The area of the quadrilateral formed by tangents at the end points of latus recta of the ellipse $$\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1$$ is :
A
$$\frac{{27}}{4}{\text{ uni}}{{\text{t}}^2}$$
B
$$9\,{\text{uni}}{{\text{t}}^2}$$
C
$$\frac{{27}}{2}{\text{ uni}}{{\text{t}}^2}$$
D
$$27\,{\text{uni}}{{\text{t}}^2}$$
Answer :
$$27\,{\text{uni}}{{\text{t}}^2}$$
37. An ellipse has $$OB$$ as semi minor axis, $$F$$ and $$F'$$ its foci and the angle $$FBF'$$ is a right angle. Then the eccentricity of the ellipse is :
A
$$\frac{1}{{\sqrt 2 }}$$
B
$$\frac{1}{2}$$
C
$$\frac{1}{4}$$
D
$$\frac{1}{{\sqrt 3 }}$$
Answer :
$$\frac{1}{{\sqrt 2 }}$$
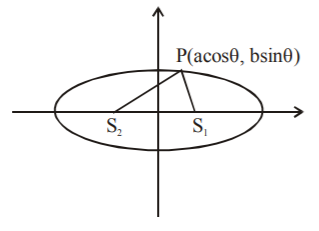
38. If a variable point $$P$$ on an ellipse of eccentricity $$e$$ is joined to the foci $${S_1}$$ and $${S_2}$$ then the incentre of the triangle $$P{S_1}{S_2}$$ lies on :
A
The major axis of the ellipse
B
The circle with radius $$e$$
C
Another ellipse of eccentricity $$\sqrt {\frac{{3 + {e^2}}}{4}} $$
D
None of these
Answer :
Another ellipse of eccentricity $$\sqrt {\frac{{3 + {e^2}}}{4}} $$
39. The slope of the diameter of the ellipse $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,$$ whose length is the GM of the major and minor axes, is :
A
$$\sqrt {\frac{a}{b}} $$
B
$$\sqrt {ab} $$
C
$$\sqrt {\frac{b}{a}} $$
D
$$\frac{a}{b}$$
Answer :
$$\sqrt {\frac{b}{a}} $$
40. If $$P\left( \theta \right)$$ and $$Q\left( {\frac{\pi }{2} + \theta } \right)$$ are two points on the ellipse $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,$$ then locus of the mid-point of $$PQ$$ is :
A
$$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = \frac{1}{2}$$
B
$$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 4$$
C
$$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 2$$
D
None of these
Answer :
$$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = \frac{1}{2}$$