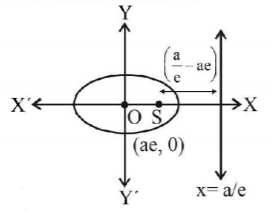
61. A focus of an ellipse is at the origin. The directrix is the line $$x=4$$ and the eccentricity is $$\frac{1}{2}.$$ Then the length of the semi-major axis is :
A
$$\frac{8}{3}$$
B
$$\frac{2}{3}$$
C
$$\frac{4}{3}$$
D
$$\frac{5}{3}$$
Answer :
$$\frac{8}{3}$$
62. If the tangents from the point $$\left( {\lambda ,\,3} \right)$$ to the ellipse $$\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1$$ are at right angles then $$\lambda $$ is :
A
$$ \pm 1$$
B
$$ \pm 3$$
C
$$ \pm 2$$
D
none of these
Answer :
$$ \pm 2$$