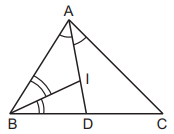
41. In a $$\vartriangle ABC,$$ $$I$$ is the incentre. The ratio $$IA : IB : IC$$ is equal to
A
$${\text{cosec}}\frac{A}{2}:{\text{cosec}}\frac{B}{2}:{\text{cosec}}\frac{C}{2}$$
B
$$\sin \frac{A}{2}:\sin \frac{B}{2}:\sin \frac{C}{2}$$
C
$$\sec \frac{A}{2}:\sec \frac{B}{2}:\sec \frac{C}{2}$$
D
None of these
Answer :
$${\text{cosec}}\frac{A}{2}:{\text{cosec}}\frac{B}{2}:{\text{cosec}}\frac{C}{2}$$
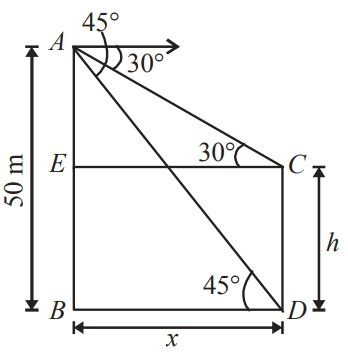
42. From the top of a cliff $$50\,m$$ high, the angles of depression of the top and bottom of a tower are observed to be $${30^ \circ }$$ and $${45^ \circ }.$$ The height of tower is
A
$$50\,m$$
B
$$50\sqrt 3 \,m$$
C
$$50\left( {\sqrt 3 - 1} \right)m$$
D
$$50\left( {1 - \frac{{\sqrt 3 }}{3}} \right)m$$
Answer :
$$50\left( {1 - \frac{{\sqrt 3 }}{3}} \right)m$$
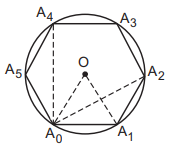
43. Let $${A_0},{A_1},{A_2},{A_3},{A_4}$$ and $${A_5}$$ be the consecutive vertices of a regular hexagon inscribed in a unit circle. The product of the lengths of $${A_0}{A_1},{A_0}{A_2}$$ and $${A_0}{A_4}$$ is
A
$$\frac{3}{4}$$
B
$${3\sqrt 3 }$$
C
$$3$$
D
$$\frac{{3\sqrt 3 }}{2}$$
Answer :
$$3$$
44. In a $$\vartriangle ABC,\left( {c + a + b} \right)\left( {a + b - c} \right) = ab.$$ The measure of $$\angle C$$ is
A
$$\frac{\pi }{3}$$
B
$$\frac{\pi }{6}$$
C
$$\frac{2\pi }{3}$$
D
None of these
Answer :
$$\frac{2\pi }{3}$$
45. In a $$\vartriangle ABC,\cos A + \cos B + \cos C > 1$$ only if the triangle is
A
acute angled
B
obtuse angled
C
right angled
D
the nature of the triangle cannot be determined
Answer :
the nature of the triangle cannot be determined
46. The number of possible triangles $$ABC$$ in which $$BC = \sqrt {11} \,cm,CA = \sqrt {13} \,cm$$ and $$A = {60^ \circ }$$ is
A
0
B
1
C
2
D
None of these
Answer :
2
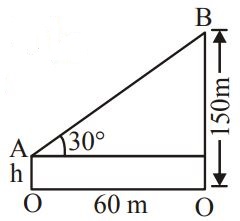
47. The horizontal distance between two towers is 60 metres and the angular depression of the top of the first tower as seen from the top of the second. is $${30^ \circ }.$$ If the height of the second tower be 150 metres, then the height of the first tower is
A
$$150 - 60\sqrt 3 \,m$$
B
$$90\,m$$
C
$$150 - 20\sqrt 3 \,m$$
D
None of these
Answer :
$$150 - 20\sqrt 3 \,m$$
48. In a $$\vartriangle ABC,2s = $$ perimeter and $$R =$$ circumradius. Then $$\frac{s}{R}$$ is equal to
A
$$\sin A + \sin B + \sin C$$
B
$$\cos A + \cos B + \cos C$$
C
$$\sin \frac{A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2}$$
D
None of these
Answer :
$$\sin A + \sin B + \sin C$$
49. In a triangle the sum of two sides is $$x$$ and the product of the same sides is $$y.$$ If $${x^2} - {c^2} = y,$$ where $$c$$ is the third side of the triangle, then the ratio of the in radius to the circum-radius of the triangle is
A
$$\frac{{3y}}{{2x\left( {x + c} \right)}}$$
B
$$\frac{{3y}}{{2c\left( {x + c} \right)}}$$
C
$$\frac{{3y}}{{4x\left( {x + c} \right)}}$$
D
$$\frac{{3y}}{{4c\left( {x + c} \right)}}$$
Answer :
$$\frac{{3y}}{{2c\left( {x + c} \right)}}$$
50. If in a $$\vartriangle ABC,2\cos A\sin C = \sin B$$ then the triangle is
A
equilateral
B
isosceles
C
right angled
D
None of these
Answer :
isosceles