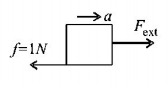
91. A block of mass $$m = 1\,kg$$ is moving with a constant acceleration $$a = 1\,m/{s^2}$$ on a rough horizontal plane. The coefficient of friction between the block and plane is $$\mu = 0.1.$$ The initial velocity of block is zero at $$t = 0.$$ The power delivered by the external agent at a time $$t = 2\,\sec$$ from the beginning is equal to (Take $$g = 10\,m/{s^2}$$ )
A
$$1\,watt$$
B
$$2\,watt$$
C
$$3\,watt$$
D
$$4\,watt$$
Answer :
$$4\,watt$$
92. If stretch in a spring of force constant $$k$$ is tripled then the ratio of elastic potential energy in the two cases will be
A
$$9:1$$
B
$$1:6$$
C
$$3:1$$
D
$$1:3$$
Answer :
$$9:1$$
93. A ball of mass $$m$$ moving with a constant velocity strikes against a ball of same mass at rest. If $$e = $$ coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A
$$\frac{{1 - e}}{{1 + e}}$$
B
$$\frac{{e - 1}}{{e + 1}}$$
C
$$\frac{{1 + e}}{{1 - e}}$$
D
$$\frac{{2 + e}}{{e - 1}}$$
Answer :
$$\frac{{1 - e}}{{1 + e}}$$
94. An athlete in the Olympic games covers a distance of $$100\,m$$ in $$10 \,s.$$ His kinetic energy can be estimated to be in the range-
A
$$200\,J-500\,J$$
B
$$2 \times {10^5}\,J - 3 \times {10^5}\,J$$
C
$$20,000\,J-50,000\,J$$
D
$$2,000\,J-5,000\,J$$
Answer :
$$2,000\,J-5,000\,J$$
95.
This question has Statement 1 and Statement 2. Of the four choices given after the Statements, choose the one that best describes the two Statements.
If two springs $${S_1}$$ and $${S_2}$$ of force constants $${k_1}$$ and $${k_2},$$ respectively, are stretched by the same force, it is found that more work is done on spring $${S_1}$$ than on spring $${S_2}.$$
STATEMENT 1 : If stretched by the same amount work done on $${S_1},$$ Work done on $${S_1}$$ is more than $${S_2}$$
STATEMENT 2 : $${k_1} < {k_2}$$
A
Statement $$1$$ is false, Statement $$2$$ is true.
B
Statement $$1$$ is true, Statement $$2$$ is false.
C
Statement $$1$$ is true, Statement $$2$$ is true, Statement $$2$$ is the correct explanation for Statement $$1$$
D
Statement $$1$$ is true, Statement $$2$$ is true, Statement $$2$$ is not the correct explanation for Statement $$1$$
Answer :
Statement $$1$$ is false, Statement $$2$$ is true.
96.
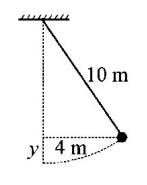
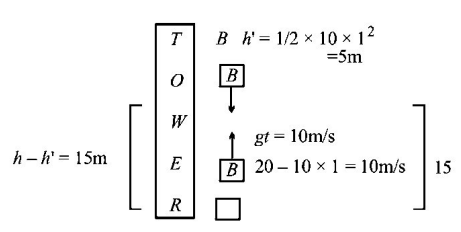
A load hangs from a travelling crane, moving horizontally with velocity $$v.$$ If the load is not to swing more than $$4m$$ horizontally, when the crane is stopped suddenly, what is the maximum allowable speed of the crane?
A
$$4.05\,m/s$$
B
$$4.00\,m/s$$
C
$$3.00\,m/s$$
D
$$3.50\,m/s$$
Answer :
$$4.05\,m/s$$
97.
An object of mass $$m$$ is projected vertically upwards with a speed of $${v_0}.$$ At the same moment another object of mass $$M,$$ which is initially above the projected one, is dropped from a height of $$h.$$ The two point like objects collide completely inelastically, and they stick to each other. Find kinetic energy (in $$J$$) of combined mass just before it hits the ground.
$$\left( {{\text{Given:}}\,m = 1\,kg,{v_0} = 20\,m/s,M = 3\,kg,h = 20\,m,g = 10\,m/{s^2}} \right)$$
A
$$550\,J$$
B
$$650\,J$$
C
$$450\,J$$
D
$$250\,J$$
Answer :
$$650\,J$$
98.
Two blocks of masses $$m$$ and $$M$$ are joined with an ideal spring of spring constant $$k$$ and kept on a rough surface as shown. The spring is initially unstretched and the coefficient of friction between the blocks and the horizontal surface is $$\mu .$$ What should be the maximum speed of the block of mass $$M$$ such that the smaller block does not move?
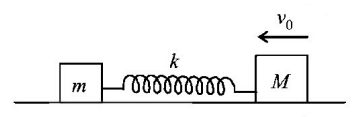
A
$$\mu g\sqrt {\frac{{Mm}}{{\left( {M + m} \right)k}}} $$
B
$$\mu g\sqrt {\frac{{\left( {M + m} \right)k}}{{Mm}}} $$
C
$$\mu g\sqrt {\frac{{\left( {2M + m} \right)m}}{{km}}} $$
D
None of these
Answer :
$$\mu g\sqrt {\frac{{\left( {2M + m} \right)m}}{{km}}} $$
99.
A $$10\,kg$$ block is pulled in the vertical plane along a frictionless surface in the form of an arc of a circle of radius $$10\,m.$$ The applied force is of $$200\,N$$ as shown in figure. If the block had started from rest at $$A,$$ the velocity at $$B$$ would be
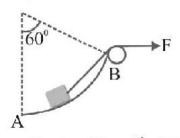
A
$$1.7\,m/s$$
B
$$17\,m/s$$
C
$$27\,m/s$$
D
$$34\,m/s$$
Answer :
$$17\,m/s$$
100. The heart of man pumps 5 litres of blood through the arteries per minute at a pressure of $$150\,mm$$ of mercury. If the density of mercury be $$13.6 \times {10^3}kg/{m^3}$$ and $$g = 10\,m/{s^2}$$ then the power of heart in watt is :
A
2.35
B
3.0
C
1.50
D
1.70
Answer :
1.70