31. The potential energy of a conservative system is given by $$U = a{y^2} - by,$$ where $$y$$ represents the position of the particle and $$a$$ as well as $$b$$ are constants. What is the force acting on the system ?
A
$$ - ay$$
B
$$ - by$$
C
$$2ay - b$$
D
$$b - 2ay$$
Answer :
$$b - 2ay$$
32.
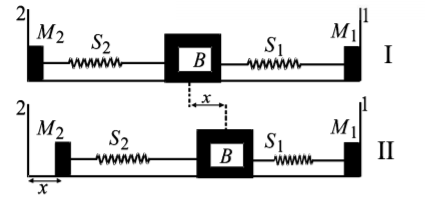
A block ($$B$$ ) is attached to two unstretched springs $${S_1}$$ and $${S_2}$$ with spring constants $$k$$ and $$4k,$$ respectively (see figure I). The other ends are attached to identical supports $${M_1}$$ and $${M_2}$$ not attached to the walls. The springs and supports have negligible mass. There is no friction anywhere. The block $$B$$ is displaced towards wall 1 by a small distance $$x$$ (figure II) and released. The block returns and moves a maximum distance $$y$$ towards wall 2. Displacements $$x$$ and $$y$$ are measured with respect to the equilibrium position of the block $$B.$$ The ratio $$\frac{y}{x}$$ is-
A
$$4$$
B
$$2$$
C
$$\frac{1}{2}$$
D
$$\frac{1}{4}$$
Answer :
$$\frac{1}{2}$$
33. A $$10\,m$$ long iron chain of linear mass density $$0.8\,kg\,{m^{ - 1}}$$ is hanging freely from a rigid support. If $$g = 10\,m{s^{ - 2}},$$ then the power required to left the chain upto the point of support in $$10$$ second
A
$$10\,W$$
B
$$20\,W$$
C
$$30\,W$$
D
$$40\,W$$
Answer :
$$40\,W$$
34. An engineer claims to have made an engine delivering $$10\,kW$$ power with fuel consumption of $$1\,g/s.$$ The calorific value of fuel is $$2\,kcal/g.$$ This claim is
A
valid
B
invalid
C
depends on engine design
D
dependent on load
Answer :
invalid
35. A bomb of mass $$30\,kg$$ at rest explodes into two pieces of masses $$18\,kg$$ and $$12\,kg.$$ The velocity of $$18\,kg$$ mass is $$6\,m{s^{ - 1}}.$$ The kinetic energy of the other mass is
A
$$256\,J$$
B
$$486\,J$$
C
$$524\,J$$
D
$$324\,J$$
Answer :
$$486\,J$$
36. The potential energy of a system increases, if work is done
A
by the system against a conservative force
B
by the system against a non-conservative force
C
upon the system by a conservative force
D
upon the system by a non-conservative force
Answer :
by the system against a conservative force
37.
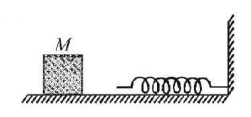
The block of mass $$M$$ moving on the frictionless horizontal surface collides with the spring of spring constant $$k$$ and compresses it by length $$L.$$ The maximum momentum of the block after collision is
A
$$\frac{{k{L^2}}}{{2M}}$$
B
$$\sqrt {Mk} L$$
C
$$\frac{{M{L^2}}}{k}$$
D
zero
Answer :
$$\sqrt {Mk} L$$
38.
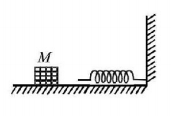
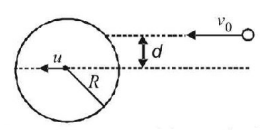
A massive disc of radius $$R$$ is moved with a constant velocity $$u$$ on a frictionless table. Another small disc collides with it elastically with a speed of $${v_0} = 0.3\,m/s,$$ the velocities of the discs being parallel. The distance $$d$$ shown in the figure is equal to $$\frac{R}{2},$$ friction between the discs is negligible. For which $$u$$ (in $$m/s$$ ) will the small disc move perpendicularly to its original motion after the collision ?
A
0.1
B
0.5
C
1.0
D
0.01
Answer :
0.1
39. A bullet of mass $$20\,g$$ and moving with $$600\,m/s$$ collides with a block of mass $$4\,kg$$ hanging with the string. What is velocity of bullet when it comes out of block, if block rises to height $$0.2\,m$$ after collision ?
A
$$200\,m/s$$
B
$$150\,m/s$$
C
$$400\,m/s$$
D
$$300\,m/s$$
Answer :
$$200\,m/s$$
40. A $$2\,kg$$ block slides on a horizontal floor with a speed of $$4\,m/s.$$ It strikes a uncompressed spring, and compresses it till the block is motionless. The kinetic friction force is $$15N$$ and spring constant is $$10,000\,N/m.$$ The spring compresses by
A
$$8.5\,cm$$
B
$$5.5\,cm$$
C
$$2.5\,cm$$
D
$$11.0\,cm$$
Answer :
$$5.5\,cm$$