41. A ball dropped from a height of $$2\,m$$ reaches to a height of $$1.5\,m$$ before hitting the ground. Then the percentage of potential energy lost is
A
25
B
30
C
50
D
100
Answer :
25
42.
A position dependent force
$$F = \left( {7 - 2x + 3{x^2}} \right)N,$$
acts on a small body of mass $$2\,kg$$ and displaces it from $$x = 0$$ to $$x = 5m.$$ Work done in joule is
A
35
B
70
C
135
D
270
Answer :
135
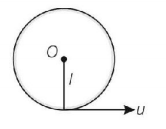
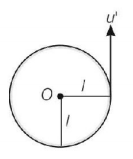
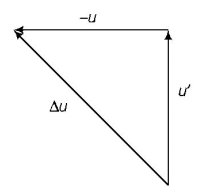
43. A stone is tied to a string of length $$l$$ and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed $$u.$$ The magnitude of the change in velocity as it reaches a position where the string is horizontal ($$g$$ being acceleration due to gravity) is
A
$$\sqrt {2\left( {{u^2} - gl} \right)} $$
B
$$\sqrt {{u^2} - gl} $$
C
$$u - \sqrt {{u^2} - 2gl} $$
D
$$\sqrt {2gl} $$
Answer :
$$\sqrt {2\left( {{u^2} - gl} \right)} $$
44. At time $$t = 0s$$ particle starts moving along the $$x$$-axis. If its kinetic energy increases uniformly with time $$t,$$ the net force acting on it must be proportional to
A
$$\sqrt t $$
B
constant
C
$$t$$
D
$$\frac{1}{{\sqrt t }}$$
Answer :
$$\frac{1}{{\sqrt t }}$$
45. A rubber ball is dropped from a height of $$5m$$ on a plane, where the acceleration due to gravity is not shown. On bouncing it rises to $$1.8\,m.$$ The ball loses its velocity on bouncing by a factor of
A
$$\frac{{16}}{{25}}$$
B
$$\frac{2}{5}$$
C
$$\frac{3}{5}$$
D
$$\frac{9}{{25}}$$
Answer :
$$\frac{2}{5}$$
46. A body falls freely under gravity. Its velocity is $$v$$ when it has lost potential energy equal to $$U.$$ What is the mass of the body?
A
$$\frac{{{U^2}}}{{{v^2}}}$$
B
$$\frac{{2{U^2}}}{{{v^2}}}$$
C
$$\frac{{2U}}{{{v^2}}}$$
D
$$\frac{U}{{{v^2}}}$$
Answer :
$$\frac{{2U}}{{{v^2}}}$$
47. A collision occurs between two identical balls of mass $$m$$ each, moving with velocities $${\overrightarrow u _1}$$ and $${\overrightarrow u _2}.$$ If the collision is head on and the energy lost in the collision is $$\Delta E = \frac{3}{{16}}{\left( {{{\overrightarrow u }_1} - {{\overrightarrow u }_2}} \right)^2}$$ then the coefficient of restitution is
A
0.25
B
0.75
C
0.5
D
0.9
Answer :
0.5
48. The energy content of gasoline is $$3.6 \times {10^7}\,J/L.$$ A motor with an efficiency of $$20\% $$ is needed at full output power of $$45\,kW$$ for $$50.0$$ minutes. How many litres of gasoline are required to operate the motor for this amount of time ?
A
$$0.31\,L$$
B
$$0.38\,L$$
C
$$1.6\,L$$
D
$$19\,L$$
Answer :
$$19\,L$$
49. The work done by a force $$\overrightarrow F = \left( { - 6{x^3}\hat i} \right)N,$$ displacing a particle from $$x = 4\,m$$ to $$x = - 2\,m$$ is
A
$$360\,J$$
B
$$240\,J$$
C
$$-240\,J$$
D
$$-360\,J$$
Answer :
$$360\,J$$
50.
An escalator has $$2400\,W$$ of power available to move passengers from the first floor of a mall to the second, $$6.0\,m$$ vertically. If the average mass of the passengers is $$65\,kg,$$ what is the maximum number of passengers that can be carried to the second floor in $$1.0$$ minute?
A
4
B
5
C
22
D
37
Answer :
37