71. The heart of a man pumps $$5 L$$ of blood through the arteries per minute at a pressure of $$150\,mm$$ of mercury. If the density of mercury be $$13.6 \times {10^3}kg/{m^3}$$ and $$g = 10\,m/{s^2},$$ then the power of heart in watt is
A
1.70
B
2.35
C
3.0
D
1.50
Answer :
1.70
72. A uniform chain of length $$2 \,m$$ is kept on a table such that a length of $$60 \,cm$$ hangs freely from the edge of the table. The total mass of the chain is $$4 \,kg.$$ What is the work done in pulling the entire chain on the table ?
A
$$12 \,J$$
B
$$3.6 \,J$$
C
$$7.2 \,J$$
D
$$1200 \,J$$
Answer :
$$3.6 \,J$$
73. A body of mass $$1\,kg$$ begins to move under the action of a time dependent force $$F = \left( {2t\,\hat i + 3{t^2}\hat j} \right)N,$$ where $${\hat i}$$ and $${\hat j}$$ are unit vectors along $$X$$ and $$Y$$ axes. What power will be developed by the force at the time $$\left( t \right)$$ ?
A
$$\left( {2{t^2} + 4{t^4}} \right)W$$
B
$$\left( {2{t^3} + 3{t^4}} \right)W$$
C
$$\left( {2{t^3} + 3{t^5}} \right)W$$
D
$$\left( {2t + 3{t^3}} \right)W$$
Answer :
$$\left( {2{t^3} + 3{t^5}} \right)W$$
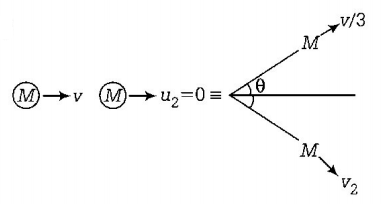
74. On a frictionless surface, a block of mass $$M$$ moving at speed $$v$$ collides elastically with another block of same mass $$M$$ which is initially at rest. After collision the first block moves at an angle $$\theta $$ to its initial direction and has a speed $$\frac{v}{3}.$$ The second block's speed after the collision is
A
$$\frac{{2\sqrt 2 }}{3}v$$
B
$$\frac{3}{4}v$$
C
$$\frac{3}{{\sqrt 2 }}v$$
D
$$\frac{{\sqrt 3 }}{2}v$$
Answer :
$$\frac{{2\sqrt 2 }}{3}v$$
75.
A block of mass $$m$$ is suspended by a light thread from a lift. The lift is moving upward with uniform velocity $$v.$$ From the frame of lift, the work done by tension on the block in $$t$$ seconds will be
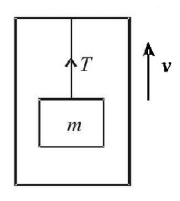
A
$$ - mgvt$$
B
$$0$$
C
$$\frac{{mgvt}}{2}$$
D
$${mgvt}$$
Answer :
$$0$$
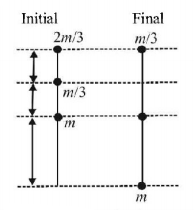
76.
Two objects each of mass $$m$$ are connected with a uniform rope having same mass $$m$$ and length $$\ell = \frac{{10}}{3}m$$ are shown in the figure. The rope can slide on a frictionless pulley which is fixed to the edge of the table. Initially $$\frac{1}{3}$$ of the rope hangs vertically. Friction is negligible everywhere.
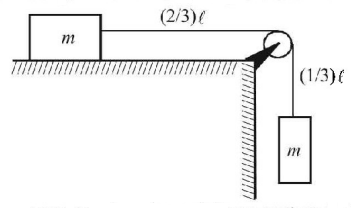
If the system is released from rest and object on the right hand side descend further by a distance of $$\frac{\ell }{3},$$ what would be the speed of the object (in $$m/s$$ )?
A
$$2.12\,m/s$$
B
$$3.33\,m/s$$
C
$$0.33\,m/s$$
D
$$4.12\,m/s$$
Answer :
$$3.33\,m/s$$
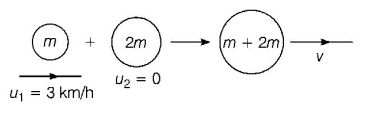
77. A body of mass $$m$$ moving with velocity $$3\,km/h$$ collides with a body of mass $$2 m$$ at rest. Now, the coalesced mass starts to move with a velocity
A
$$1\,km/h$$
B
$$2\,km/h$$
C
$$3\,km/h$$
D
$$4\,km/h$$
Answer :
$$1\,km/h$$
78. A force acts on a $$3.0\,g$$ particle in such a way that the position of the particle as a function of time is given by $$x = 3t - 4{t^2} + {t^3},$$ where $$x$$ is in metre and $$t$$ in second. The work done during the first $$4\,s$$ is
A
$$570\,mJ$$
B
$$450\,mJ$$
C
$$490\,mJ$$
D
$$528\,mJ$$
Answer :
$$528\,mJ$$
79. A ball is thrown vertically downwards from a height of $$20\,m$$ with an initial velocity $${v_0}.$$ It collides with the ground, loses $$50\% $$ of its energy in collision and rebounds to the same height. The initial velocity $${v_0}$$ is (Take, $$g = 10\,m{s^{ - 2}}$$ )
A
$$14\,m{s^{ - 1}}$$
B
$$20\,m{s^{ - 1}}$$
C
$$28\,m{s^{ - 1}}$$
D
$$10\,m{s^{ - 1}}$$
Answer :
$$20\,m{s^{ - 1}}$$
80.
A bead of mass $$m$$ is sliding down the fixed inclined rod without friction. It is connected to a point $$P$$ on the horizontal surface with a light spring of spring constant $$k.$$ The bead is initially released from rest and the spring is initially unstressed and vertical. The bead just stops at the bottom of the inclined rod. Find the angle which the inclined rod makes with horizontal.
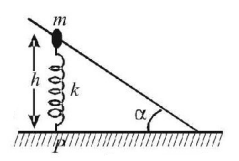
A
$${\cot ^{ - 1}}\left( {1 + \sqrt {\frac{{2mg}}{{kh}}} } \right)$$
B
$${\tan ^{ - 1}}\left( {1 + \sqrt {\frac{{2mg}}{{kh}}} } \right)$$
C
$${\cot ^{ - 1}}\left( {1 + \sqrt {\frac{{mg}}{{kh}}} } \right)$$
D
$${\tan ^{ - 1}}\left( {1 + \sqrt {\frac{{mg}}{{kh}}} } \right)$$
Answer :
$${\cot ^{ - 1}}\left( {1 + \sqrt {\frac{{2mg}}{{kh}}} } \right)$$