221.
Let $${f\left( x \right)}$$ be a polynomial of degree four having extreme values at $$x = 1$$ and $$x = 2.$$ If $$\mathop {\lim }\limits_{x \to 0} \left[ {1 + \frac{{f\left( x \right)}}{{{x^2}}}} \right] = 3,$$ then $$f\left( 2 \right)$$ is equal to:
A
0
B
4
C
- 8
D
- 4
Answer :
0
View Solution
$$\eqalign{
& \mathop {\lim }\limits_{x \to 0} \left[ {1 + \frac{{f\left( x \right)}}{{{x^2}}}} \right] = 3, \Rightarrow \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right)}}{{{x^2}}} = 2 \cr
& {\text{So,}}\,f\left( x \right)\,{\text{contains terms in }}{x^2},{x^3}\,{\text{and }}{x^4}{\text{.}} \cr
& {\text{Let }}f\left( x \right) = {a_1}{x^2} + {a_2}{x^3} + {a_3}{x^4} \cr
& {\text{since }}\mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right)}}{{{x^2}}} = 2 \Rightarrow {a_1} = 2 \cr
& {\text{Hence, }}f\left( x \right) = 2{x^2} + {a_2}{x^3} + {a_3}{x^4} \cr
& f'\left( x \right) = 4x + 3{a_2}{x^2} + 4{a_3}{x^3} \cr
& {\text{As given }}:f'\left( 1 \right) = 0{\text{ and }}f'\left( 2 \right) = 0 \cr
& {\text{Hence, }}4 + 3{a_2} + 4{a_3} = 0\,......\left( 1 \right) \cr
& {\text{and }}8 + 12{a_2} + 32{a_3} = 0\,......\left( 2 \right) \cr
& {\text{By}}\,4x\left( {{\text{eq}}1} \right) - {\text{eq}}\left( 2 \right),\,{\text{we get}} \cr
& 16 + 12{a_2} + 16{a_3} - \left( {8 + 12{a_2} + 32{a_3}} \right) = 0 \cr
& \Rightarrow 8 - 16{a_3} = 0 \Rightarrow {a_3} = \frac{1}{2} \cr
& {\text{and by eqn}}{\text{. }}\left( 1 \right),4 + 3{a_2} + \frac{4}{2} = 0 \Rightarrow {a_2} = - 2 \cr
& \Rightarrow f\left( x \right) = 2{x^2} - 2{x^3} + \frac{1}{2}{x^4} \cr
& f\left( 2 \right) = 2 \times 4 - 2 \times 8 + \frac{1}{2} \times 16 = 0 \cr} $$
222.
If $$y = a\ln x + b{x^2} + x$$ has its extremum values at $$x = - 1$$ and $$x = 2,$$ then
A
$$a = 2,b = - 1$$
B
$$a = 2,b = - \frac{1}{2}$$
C
$$a = - 2,b = \frac{1}{2}$$
D
none of these
Answer :
$$a = 2,b = - \frac{1}{2}$$
View Solution
$$\eqalign{
& y = a\ln x + b{x^2} + x \cr
& {\text{has}}\,{\text{its}}\,{\text{extremum}}\,{\text{values}}\,{\text{at}}\,x = - 1\,{\text{and}}\,2 \cr
& \therefore \frac{{dy}}{{dx}} = 0\,{\text{at}}\,x = - 1\,{\text{and}}\,2 \cr
& \Rightarrow \frac{a}{x} + 2bx + 1 = 0\,{\text{or}}\,2b{x^2} + x + a = 0 \cr
& {\text{has}}\, - 1\,{\text{and}}\,2\,{\text{as}}\,{\text{its}}\,{\text{roots}}{\text{.}} \cr
& \therefore 2b - 1 + a = 0\,......\left( 1 \right) \cr
& 8b + 2 + a = 0\,......\left( 2 \right) \cr
& {\text{Solving}}\,\left( 1 \right)\,{\text{and}}\,\left( 2 \right){\text{we}}\,{\text{get}}\,a = 2,b = - \frac{1}{2} \cr} $$
223.
A spherical balloon is filled with 4500$$\pi $$ cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72$$\pi $$ cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is :
A
$$\frac{9}{7}$$
B
$$\frac{7}{9}$$
C
$$\frac{2}{9}$$
D
$$\frac{9}{2}$$
Answer :
$$\frac{2}{9}$$
View Solution
$$\eqalign{
& {\text{Volume}}\,{\text{of}}\,{\text{spherical}}\,{\text{balloon}}\, = V = \frac{4}{3}\pi {r^3} \cr
& \Rightarrow 4500\pi = \frac{{4\pi {r^3}}}{3}{\kern 1pt} \,\left( \because \right.\,{\text{Given,volume}}\,\left. { = 4500\pi {m^3}} \right) \cr
& {\text{Differentiating both the sides, w}}{\text{.r}}{\text{.t }}'t'{\text{ we get,}} \cr
& \frac{{dV}}{{dt}} = 4\pi {r^2}\left( {\frac{{dr}}{{dt}}} \right) \cr
& {\text{Now,}}\,{\text{it}}\,{\text{is}}\,{\text{given}}\,{\text{that}}\,\frac{{dV}}{{dt}} = 72\pi \cr
& \therefore {\text{After }}49{\text{ min, Volume}} \cr
& \, = \left( {4500 - 49 \times 72} \right)\pi \cr
& = \left( {4500 - 3528} \right)\pi \cr
& = 972\pi {m^3} \cr
& \Rightarrow V = 972\pi {m^3}\,\,\,\therefore 972\pi = \frac{4}{3}\pi {r^3} \cr
& \Rightarrow {r^3} = 3 \times 243 \cr
& \Rightarrow {r^3} = 3 \times {3^5} \cr
& \Rightarrow {r^3} = {3^6} \cr
& \Rightarrow {r^3} = {\left( {{3^2}} \right)^3} \cr
& \Rightarrow r = 9 \cr
& {\text{Also,we}}\,{\text{have}}\,\frac{{dV}}{{dt}} = 72\pi \cr
& \therefore 72\pi = 4\pi \times 9 \times 9\left( {\frac{{dr}}{{dt}}} \right) \Rightarrow \frac{{dr}}{{dt}} = \left( {\frac{2}{9}} \right) \cr} $$
224.
Let $$f:R \to R$$ be a function such that $$f\left( x \right) = ax + 3\sin \,x + 4\cos \,x.$$ Then $$f\left( x \right)$$ is invertible if :
A
$$a\, \in \,\left( { - 5,\,5} \right)$$
B
$$a\, \in \,\left( { - \infty ,\, - 5} \right)$$
C
$$a\, \in \,\left( {5,\, + \infty } \right)$$
D
none of these
Answer :
$$a\, \in \,\left( { - 5,\,5} \right)$$
View Solution
$$\eqalign{
& f'\left( x \right) = a + 3\cos \,x - 4\sin \,x \cr
& = a + 5\cos \left( {x + \alpha } \right),{\text{ where }}\cos \,\alpha = \frac{3}{5} \cr
& \therefore a - 5 \leqslant f'\left( x \right) \leqslant a + 5 \cr} $$
225.
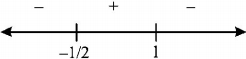
If $$f\left( x \right) = x{e^{x\left( {1 - x} \right)}},$$ then $$f\left( x \right)$$ is
A
increasing on $$\left[ { - \frac{1}{2},1} \right]$$
B
decreasing on $$R$$
C
increasing on $$R$$
D
decreasing on $$\left[ { - \frac{1}{2},1} \right]$$
Answer :
increasing on $$\left[ { - \frac{1}{2},1} \right]$$
View Solution
$$\eqalign{
& f\left( x \right) = x{e^{x\left( {1 - x} \right)}} \cr
& \Rightarrow f'\left( x \right) = {e^{x\left( {1 - x} \right)}} + \left( {1 - 2x} \right)x{e^{x\left( {1 - x} \right)}} \cr
& = - {e^{x\left( {1 - x} \right)}} + \left( {2{x^2} - x - 1} \right) = - {e^{x\left( {1 - x} \right)}} + \left( {2x + 1} \right)\left( {x - 1} \right) \cr} $$
$$\therefore \,\,\,f\left( x \right)$$ is increasing on $$\left[ { - \frac{1}{2},1} \right]$$
226.
The equation $$\sin \,x + x\cos \,x = 0$$ has at least one root in the interval :
A
$$\left( { - \frac{\pi }{2},\,0} \right)$$
B
$$\left( {0,\,\pi } \right)$$
C
$$\left( { - \frac{\pi }{2},\,\frac{\pi }{2}} \right)$$
D
none of these
Answer :
$$\left( {0,\,\pi } \right)$$
View Solution
$$\eqalign{
& \int {\left( {\sin \,x + x\cos \,x} \right)dx} = - \cos \,x + \int {x\cos \,x\,dx} \cr
& = - \cos \,x + \left\{ {x\sin \,x - \int {\sin \,x\,dx} } \right\} \cr
& = - \cos \,x + x\sin \,x + \cos \,x \cr
& = x\sin \,x \cr} $$