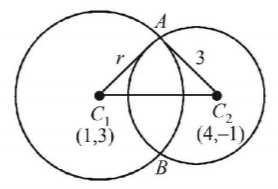
91. If the two circles $${\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = {r^2}$$ and $${x^2} + {y^2} - 8x + 2y + 8 = 0$$ intersect in two distinct points, then-
A
$$2 < r < 8$$
B
$$r < 2$$
C
$$r = 2$$
D
$$r > 2$$
Answer :
$$2 < r < 8$$
92. The range of values of $$r$$ for which the point $$\left( { - 5 + \frac{r}{{\sqrt 2 }},\, - 3 + \frac{r}{{\sqrt 2 }}} \right)$$ is an interior point of the major segment of the circle $${x^2} + {y^2} = 16,$$ cut off by the line $$x + y = 2,$$ is :
A
$$\left( { - \infty ,\,5\sqrt 2 } \right)$$
B
$$\left( {4\sqrt 2 - \sqrt {14} ,\,5\sqrt 2 } \right)$$
C
$$\left( {4\sqrt 2 - \sqrt {14} ,\,4\sqrt 2 + \sqrt {14} } \right)$$
D
none of these
Answer :
$$\left( {4\sqrt 2 - \sqrt {14} ,\,5\sqrt 2 } \right)$$
93. If a tangent to the circle $${x^2} + {y^2} = 1$$ intersects the coordinate axes at distinct points $$P$$ and $$Q,$$ then the locus of the mid-point of $$PQ$$ is:
A
$${x^2} + {y^2} - 4{x^2}{y^2} = 0$$
B
$${x^2} + {y^2} - 2xy = 0$$
C
$${x^2} + {y^2} - 16{x^2}{y^2} = 0$$
D
$${x^2} + {y^2} - 2{x^2}{y^2} = 0$$
Answer :
$${x^2} + {y^2} - 4{x^2}{y^2} = 0$$
94. The locus of the centre of a circle, which touches externally the circle $${x^2} + {y^2} - 6x - 6y + 14 = 0$$ and also touches the $$y$$-axis, is given by the equation :
A
$${x^2} - 6x - 10y + 14 = 0$$
B
$${x^2} - 10x - 6y + 14 = 0$$
C
$${y^2} - 6x - 10y + 14 = 0$$
D
$${y^2} - 10x - 6y + 14 = 0$$
Answer :
$${y^2} - 10x - 6y + 14 = 0$$
95. The range of values of $$a$$ for which the point $$\left( {a,\,4} \right)$$ is outside the circles $${x^2} + {y^2} + 10x = 0$$ and $${x^2} + {y^2} - 12x + 20 = 0$$ is :
A
$$\left( { - \infty ,\, - 8} \right) \cup \left( { - 2,\,6} \right) \cup \left( {6,\, + \infty } \right)$$
B
$$\left( { - 8,\, - 2} \right)$$
C
$$\left( { - \infty ,\, - 8} \right) \cup \left( { - 2,\, + \infty } \right)$$
D
none of these
Answer :
$$\left( { - \infty ,\, - 8} \right) \cup \left( { - 2,\,6} \right) \cup \left( {6,\, + \infty } \right)$$
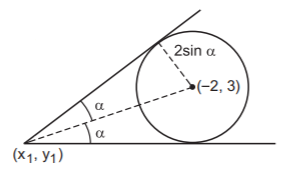
96. The angle between a pair of tangents drawn from a point $$P$$ to the curve $${x^2} + {y^2} + 4x - 6y + 9{\sin ^2}\alpha + 13{\cos ^2}\alpha = 0$$ is $$2\alpha .$$ The locus of $$P$$ is :
A
$${x^2} + {y^2} + 4x - 6y + 4 = 0$$
B
$${x^2} + {y^2} + 4x - 6y - 9 = 0$$
C
$${x^2} + {y^2} + 4x - 6y - 4 = 0$$
D
$${x^2} + {y^2} + 4x - 6y + 9 = 0$$
Answer :
$${x^2} + {y^2} + 4x - 6y + 9 = 0$$
97. The point $$\left( {\left[ {P + 1} \right],\,\left[ P \right]} \right)$$ (where $$\left[ x \right]$$ is the greatest integer less than or equal to $$x$$), lying inside the region bounded by the circle $${x^2} + {y^2} - 2x - 15 = 0$$ and $${x^2} + {y^2} - 2x - 7 = 0,$$ then :
A
$$P\, \in \left[ { - 1,\,0} \right) \cup \left[ {0,\,1} \right) \cup \left[ {1,\,2} \right)$$
B
$$P\, \in \left[ { - 1,\,2} \right) - \left\{ {0,\,1} \right\}$$
C
$$P\, \in \left( { - 1,\,2} \right)$$
D
none of these
Answer :
none of these
98. The equations of two circles are $${x^2} + {y^2} - 26y + 25 = 0$$ and $${x^2} + {y^2} = 25.$$ Then :
A
they touch each other
B
they cut each other orthogonally
C
one circle is inside the other circle
D
none of these
Answer :
they cut each other orthogonally
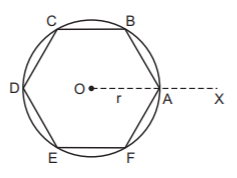
99. The point $$P$$ moves in the plane of a regular hexagon such that the sum of the squares of its distances from the vertices of the hexagon is $$6{a^2}.$$ If the radius of the circumcircle of the hexagon is $$r\left( { < a} \right)$$ then the locus of $$P$$ is :
A
a pair of straight lines
B
an ellipse
C
a circle of radius $$\sqrt {{a^2} - {r^2}} $$
D
an ellipse of major axis $$a$$ and minor axis $$r$$
Answer :
a circle of radius $$\sqrt {{a^2} - {r^2}} $$
100. If the two circles $${\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = {r^2}$$ and $${x^2} + {y^2} - 8x + 2y + 8 = 0$$ intersect in two distinct point, then-
A
$$r > 2$$
B
$$2 < r < 8$$
C
$$r < 2$$
D
$$r = 2$$
Answer :
$$2 < r < 8$$