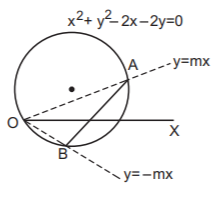
101. The equation of the locus of the middle point of a chord of the circle $${x^2} + {y^2} = 2\left( {x + y} \right)$$ such that the pair of lines joining the origin to the point of intersection of the chord and the circle are equally inclined to the $$x$$-axis is :
A
$$x + y = 2$$
B
$$x - y = 2$$
C
$$2x - y = 1$$
D
none of these
Answer :
$$x + y = 2$$
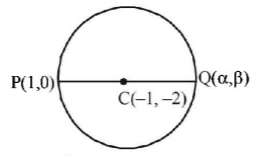
102. The point diametrically opposite to the point $$P\left( {1,\,0} \right)$$ on the circle $${x^2} + {y^2} + 2x + 4y - 3 = 0$$ is-
A
$$\left( {3,\, - 4} \right)$$
B
$$\left( { - 3,\,4} \right)$$
C
$$\left( { - 3,\, - 4} \right)$$
D
$$\left( {3,\,4} \right)$$
Answer :
$$\left( { - 3,\, - 4} \right)$$
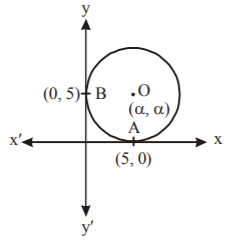
103. The equation of the circle which touches the axes at a distance $$5$$ from the origin is $${y^2} + {x^2} - 2\alpha x - 2\alpha y + {\alpha ^2} = 0.$$ What is the value of $$\alpha \,?$$
A
$$4$$
B
$$5$$
C
$$6$$
D
$$7$$
Answer :
$$5$$
104. The number of common tangents to the circles $${x^2} + {y^2} - 4x - 6y - 12 = 0$$ and $${x^2} + {y^2} + 6x + 18y + 26 = 0$$ is :
A
$$3$$
B
$$4$$
C
$$1$$
D
$$2$$
Answer :
$$3$$
105. The equation $${x^2} + {y^2} - 2x + 4y + 5 = 0$$ represents :
A
a point
B
a pair of straight lines
C
a circle of nonzero radius
D
none of these
Answer :
a point
106. The locus of a point from which the lengths of the tangents to the circles $${x^2} + {y^2} = 4$$ and $$2\left( {{x^2} + {y^2}} \right) - 10x + 3y - 2 = 0$$ are equal is :
A
a straight line inclined at $$\frac{\pi }{4}$$ with the line joining the centres of the circles
B
a circle
C
an ellipse
D
a straight line perpendicular to the line joining the centres of the circles
Answer :
a straight line perpendicular to the line joining the centres of the circles
107. Let $$f\left( {x,\,y} \right) = 0$$ be the equation of a circle. If $$f\left( {0,\,\lambda } \right) = 0$$ has equal roots $$\lambda = 2,\,2,$$ and $$f\left( {\lambda ,\,0} \right) = 0$$ has roots $$\lambda = \frac{4}{5},\,5$$ then the centre of the circle is :
A
$$\left( {2,\,\frac{{29}}{{10}}} \right)$$
B
$$\left( {\frac{{29}}{{10}},\,2} \right)$$
C
$$\left( { - 2,\,\frac{{29}}{{10}}} \right)$$
D
none of these
Answer :
$$\left( {\frac{{29}}{{10}},\,2} \right)$$
108. The equation of any tangent to the circle $${x^2} + {y^2} - 2x + 4y - 4 = 0$$ is :
A
$$y = m\left( {x - 1} \right) + 3\sqrt {1 + {m^2}} - 2$$
B
$$y = mx + 3\sqrt {1 + {m^2}} $$
C
$$y = mx + 3\sqrt {1 + {m^2}} - 2$$
D
none of these
Answer :
$$y = m\left( {x - 1} \right) + 3\sqrt {1 + {m^2}} - 2$$
109. If the circles $${x^2} + {y^2} + 2x + 2ky + 6 = 0,\,\,{x^2} + {y^2} + 2ky + k = 0$$ intersect orthogonally, then $$k$$ is-
A
$$2\,\,{\text{or }} - \frac{3}{2}$$
B
$$ - 2\,\,{\text{or }} - \frac{3}{2}$$
C
$$2\,\,{\text{or }}\frac{3}{2}$$
D
$$ - 2\,\,{\text{or }}\frac{3}{2}$$
Answer :
$$2\,\,{\text{or }} - \frac{3}{2}$$
110. The locus of the centres of circles passing through the origin and intersecting the fixed circle $${x^2} + {y^2} - 5x + 3y - 1 = 0$$ orthogonally is :
A
a straight line of the slope $$\frac{3}{5}$$
B
a circle
C
a pair of straight lines
D
none of these
Answer :
none of these