41. If (2, 4) is a point interior to the circle $${x^2} + {y^2} - 6x - 10y + \lambda = 0$$ and the circle does not cut the axes at any point then $$\lambda $$ belongs to the interval :
A
$$\left( {25,\,32} \right)$$
B
$$\left( {9,\,32} \right)$$
C
$$\left( {32,\, + \infty } \right)$$
D
none of these
Answer :
$$\left( {25,\,32} \right)$$
42. Two circles have the equations $${x^2} + {y^2} - 4x - 6y - 8 = 0$$ and $${x^2} + {y^2} - 2x - 3 = 0.$$ Then :
A
they cut each other
B
they touch each other
C
one circle lies inside the other
D
one circle lies wholly outside the other
Answer :
they cut each other
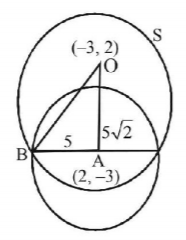
43. If one of the diameters of the circle, given by the equation, $${x^2} + {y^2} - 4x + 6y - 12 = 0,$$ is a chord of a circle $$S,$$ whose centre is at ($$-$$ 3, 2), then the radius of $$S$$ is:
A
$$5$$
B
$$10$$
C
$$5\sqrt 2 $$
D
$$5\sqrt 3 $$
Answer :
$$5\sqrt 3 $$
44. The number of common tangents to the circles $${x^2} + {y^2} = 4$$ and $${x^2} + {y^2} - 6x - 8y = 24$$ is :
A
$$0$$
B
$$1$$
C
$$3$$
D
$$4$$
Answer :
$$1$$
45. The locus of the centres of the circles for which one end of a diameter is (1, 1) while the other end is on the line $$x + y = 3$$ is :
A
$$x + y = 1$$
B
$$2\left( {x - y} \right) = 5$$
C
$$2x + 2y = 5$$
D
none of these
Answer :
$$2x + 2y = 5$$
46. A square is inscribed in the circle $${x^2} + {y^2} - 2x + 4y + 3 = 0.$$ Its sides are parallel to the coordinate axes. The one vertex of the square is-
A
$$\left( {1 + \sqrt 2 ,\, - 2 } \right)$$
B
$$\left( {1 - \sqrt 2 ,\, - 2 } \right)$$
C
$$\left( {1 - 2 ,\, + \sqrt 2 } \right)$$
D
none of these
Answer :
none of these
47. If the lines $$2x+3y+1=0$$ and $$3x-y-4=0$$ lie along diameter of a circle of circumference $$10\pi ,$$ then the equation of the circle is-
A
$${x^2} + {y^2} + 2x - 2y - 23 = 0$$
B
$${x^2} + {y^2} - 2x - 2y - 23 = 0$$
C
$${x^2} + {y^2} + 2x + 2y - 23 = 0$$
D
$${x^2} + {y^2} - 2x + 2y - 23 = 0$$
Answer :
$${x^2} + {y^2} - 2x + 2y - 23 = 0$$
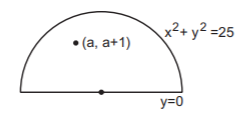
48. A region in the $$x$$-$$y$$ plane is bounded by the curve $$y = \sqrt {25 - {x^2}} $$ and the line $$y=0.$$ If the point $$\left( {a,\,a + 1} \right)$$ lies in the interior of the region then :
A
$$a\, \in \,\left( { - 4,\,3} \right)$$
B
$$a\, \in \,\left( { - \infty ,\, - 1} \right) \cup \left( {3,\, + \infty } \right)$$
C
$$a\, \in \,\left( { - 1,\,3} \right)$$
D
none of these
Answer :
$$a\, \in \,\left( { - 1,\,3} \right)$$
49. If the centre of the circle passing through the origin is $$\left( {3,\,4} \right),$$ then the intercepts cut off by the circle on $$x$$-axis and $$y$$-axis respectively are :
A
$$3$$ units and $$4$$ units
B
$$6$$ units and $$4$$ units
C
$$3$$ units and $$8$$ units
D
$$6$$ units and $$8$$ units
Answer :
$$6$$ units and $$8$$ units
50. The number of integral values of $$\lambda $$ for which $${x^2} + {y^2} + \lambda x + \left( {1 - \lambda } \right)y + 5 = 0$$ is the equation of a circle whose radius cannot exceed 5, is :
A
$$14$$
B
$$18$$
C
$$16$$
D
none of these
Answer :
$$16$$