81. If one of the diameters of the circle $${x^2} + {y^2} - 2x - 6y + 6 = 0$$ is a chord to the circle with centre (2, 1), then the radius of the circle is-
A
$$\sqrt 3 $$
B
$$\sqrt 2 $$
C
$$3$$
D
$$2$$
Answer :
$$3$$
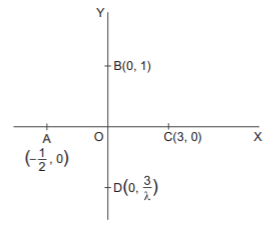
82. If the common chord of the circles $${x^2} + {\left( {y - \lambda } \right)^2} = 16$$ and $${x^2} + {y^2} = 16$$ subtend a right angle at the origin then $$\lambda $$ is equal to :
A
$$4$$
B
$$4\sqrt 2 $$
C
$$ \pm 4\sqrt 2 $$
D
$$8$$
Answer :
$$ \pm 4\sqrt 2 $$
83. If polar of a circle $${x^2} + {y^2} = {a^2}$$ with respect to $$\left( {x',\,y'} \right)$$ is $$Ax + By + C = 0,$$ then its pole will be :
A
$$\left( {\frac{{{a^2}A}}{{ - C}},\,\frac{{{a^2}B}}{{ - C}}} \right)$$
B
$$\left( {\frac{{{a^2}A}}{C},\,\frac{{{a^2}B}}{C}} \right)$$
C
$$\left( {\frac{{{a^2}C}}{A},\,\frac{{{a^2}C}}{B}} \right)$$
D
$$\left( {\frac{{{a^2}C}}{{ - A}},\,\frac{{{a^2}C}}{{ - B}}} \right)$$
Answer :
$$\left( {\frac{{{a^2}A}}{{ - C}},\,\frac{{{a^2}B}}{{ - C}}} \right)$$
84. A ray of light incident at the point $$\left( { - 2,\, - 1} \right)$$ gets reflected from the tangent at $$\left( {0,\, - 1} \right)$$ to the circle $${x^2} + {y^2} = 1.$$ The reflected ray touches the circle. The equation of the line along which the incident ray moved is :
A
$$4x - 3y + 11 = 0$$
B
$$4x + 3y + 11 = 0$$
C
$$3x + 4y + 11 = 0$$
D
none of these
Answer :
$$4x + 3y + 11 = 0$$
85. The intercept on the line $$y=x$$ by the circle $${x^2} + {y^2} - 2x = 0$$ is $$AB.$$ The equation of the circle with $$AB$$ as a diameter is :
A
$${x^2} + {y^2} + x + y = 0$$
B
$${x^2} + {y^2} = x + y$$
C
$${x^2} + {y^2} - 3x + y = 0$$
D
none of these
Answer :
$${x^2} + {y^2} = x + y$$
86. If a circle passes through the points of intersection of the lines $$2x - y + 1 = 0$$ and $$x + \lambda y - 3 = 0$$ with the axes of reference then the value of $$\lambda $$ is :
A
$$\frac{1}{2}$$
B
$$2$$
C
$$1$$
D
$$-2$$
Answer :
$$-2$$
87. The lines $$2x-3y=5$$ and $$3x-4y=7$$ are diameters of a circle having area as $$154$$ square units. Then the equation of the circle is-
A
$${x^2} + {y^2} - 2x + 2y = 62$$
B
$${x^2} + {y^2} + 2x - 2y = 62$$
C
$${x^2} + {y^2} + 2x - 2y = 47$$
D
$${x^2} + {y^2} - 2x + 2y = 47$$
Answer :
$${x^2} + {y^2} - 2x + 2y = 47$$
88. The members of a family of circles are given by the equation $$2\left( {{x^2} + {y^2}} \right) + \lambda x - \left( {1 + {\lambda ^2}} \right)y - 10 = 0.$$ The number of circles belonging to the family that are cut orthogonally by the fixed circle $${x^2} + {y^2} + 4x + 6y + 3 = 0$$ is :
A
2
B
1
C
0
D
none of these
Answer :
2
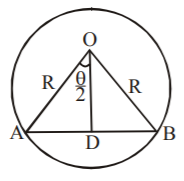
89. Consider a circle of radius $$R$$. What is the length of a chord which subtends an angle $$\theta $$ at the centre ?
A
$$2R\,\sin \left( {\frac{\theta }{2}} \right)$$
B
$$2R\,\sin \,\theta $$
C
$$2R\,\tan \left( {\frac{\theta }{2}} \right)$$
D
$$2R\,\tan \,\theta $$
Answer :
$$2R\,\sin \left( {\frac{\theta }{2}} \right)$$
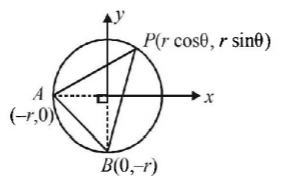
90. Let $$AB$$ be a chord of the circle $${x^2} + {y^2} = {r^2}$$ subtending a right angle at the centre. Then the locus of the centroid of the triangle $$PAB$$ as $$P$$ moves on the circle is-
A
a parabola
B
a circle
C
an ellipse
D
a pair of straight lines
Answer :
a circle