111.
If $$\sin x + \sin y = a$$ and $$\cos x + \cos y = b,$$ then $${\tan ^2}\left( {\frac{{x + y}}{2}} \right) + {\tan ^2}\left( {\frac{{x - y}}{2}} \right)$$ is equal to
A
$$\frac{{{a^4} + {b^4} + 4{b^2}}}{{{a^2}{b^2} + {b^4}}}$$
B
$$\frac{{{a^4} - {b^4} + 4{b^2}}}{{{a^2}{b^2} + {b^4}}}$$
C
$$\frac{{{a^4} - {b^4} + 4{a^2}}}{{{a^2}{b^2} + {a^4}}}$$
D
None of the above
Answer :
$$\frac{{{a^4} - {b^4} + 4{b^2}}}{{{a^2}{b^2} + {b^4}}}$$
View Solution
$$\eqalign{
& \sin x + \sin y = a \cr
& \Rightarrow 2\sin \left( {\frac{{x + y}}{2}} \right)\cos \left( {\frac{{x - y}}{2}} \right) = a\,\,\,.....\left( 1 \right) \cr
& \cos x + \cos y = b \cr
& \Rightarrow 2\cos \left( {\frac{{x + y}}{2}} \right)\cos \left( {\frac{{x - y}}{2}} \right) = b\,\,\,.....\left( 2 \right) \cr} $$
112.
If $$3\sin \theta + 4\cos \theta = 5$$ then the value of $$4\sin \theta - 3\cos \theta $$ is
A
0
B
5
C
1
D
None of these
Answer :
0
View Solution
$$\eqalign{
& {\left( {3\sin \theta + 4\cos \theta } \right)^2} + {\left( {4\sin \theta - 3\cos \theta } \right)^2} = 16 + 9 = 25 \cr
& \therefore \,\,25 + {\left( {4\sin \theta - 3\cos \theta } \right)^2} = 25 \cr
& \therefore \,\,4\sin \theta - 3\cos \theta = 0. \cr} $$
113.
If $$A = {\sin ^2}x + {\cos ^4}x,$$ then for all real $$x$$:
A
$$\frac{{13}}{{16}} \leqslant A \leqslant 1$$
B
$$1 \leqslant A \leqslant 2$$
C
$$\frac{3}{4} \leqslant A \leqslant \frac{{13}}{{16}}$$
D
$$\frac{{3}}{{4}} \leqslant A \leqslant 1$$
Answer :
$$\frac{{3}}{{4}} \leqslant A \leqslant 1$$
View Solution
$$\eqalign{
& A = {\sin ^2}x + {\cos ^4}x \cr
& = {\sin ^2}x + {\cos ^2}x\left( {1 - {{\sin }^2}x} \right) \cr
& = {\sin ^2}x + {\cos ^2}x - \frac{1}{4}{\left( {2\sin x.\cos x} \right)^2} \cr
& = 1 - \frac{1}{4}{\sin ^2}\left( {2x} \right) \cr
& {\text{Now }}0 \leqslant {\sin ^2}\left( {2x} \right) \leqslant 1 \cr
& \Rightarrow \,\,0 \geqslant - \frac{1}{4}{\sin ^2}\left( {2x} \right) \geqslant - \frac{1}{4} \cr
& \Rightarrow \,\,1 \geqslant 1 - \frac{1}{4}{\sin ^2}\left( {2x} \right) \geqslant 1 - \frac{1}{4} \cr
& \Rightarrow \,\,1 \geqslant A \geqslant \frac{3}{4} \cr} $$
114.
Given $$A = {\sin ^2}\theta + {\cos ^4}\theta $$ then for all real values of $$\theta $$
A
$$1 \leqslant A \leqslant 2$$
B
$$\frac{3}{4} \leqslant A \leqslant 1$$
C
$$\frac{13}{16} \leqslant A \leqslant 1$$
D
$$\frac{3}{4} \leqslant A \leqslant \frac{{13}}{{16}}$$
Answer :
$$\frac{3}{4} \leqslant A \leqslant 1$$
View Solution
$$\eqalign{
& A = {\sin ^2}\theta + {\cos ^4}\theta \cr
& = {\sin ^2}\theta + {\left( {1 - {{\sin }^2}\theta } \right)^2} \cr
& = {\sin ^4}\theta - {\sin ^2}\theta + 1 \cr
& \Rightarrow \,\,A = {\left( {{{\sin }^2}\theta - \frac{1}{2}} \right)^2} + \frac{3}{4} \cr
& {\text{But }}0 \leqslant {\left( {{{\sin }^2}\theta - \frac{1}{2}} \right)^2} \leqslant \frac{1}{4} \cr
& \therefore \,\,\frac{3}{4} \leqslant {\left( {{{\sin }^2}\theta - \frac{1}{2}} \right)^2} + \frac{3}{4} \leqslant 1\,\,{\text{or }}\frac{3}{4} \leqslant A \leqslant 1 \cr} $$
115.
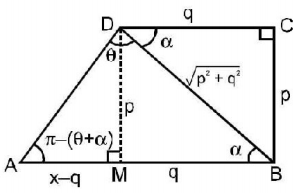
$$ABCD$$ is a trapezium such that $$AB$$ and $$CD$$ are parallel and $${{BC}} \bot {{CD}}{{.}}$$ If $$\angle {{ADB}} = \theta ,$$ $$BC = p$$ and $$CD = q,$$ then $$AB$$ is equal to:
A
$$\frac{{\left( {{p^2} + {q^2}} \right)\sin \theta }}{{p\cos \theta + q\sin \theta }}$$
B
$$\frac{{{p^2} + {q^2}\cos \theta }}{{p\cos \theta + q\sin \theta }}$$
C
$$\frac{{{p^2} + {q^2}\cos \theta }}{{{p^2}\cos \theta + {q^2}\sin \theta }}$$
D
$$\frac{{\left( {{p^2} + {q^2}} \right)\sin \theta }}{{{{\left( {p\cos \theta + q\sin \theta } \right)}^2}}}$$
Answer :
$$\frac{{\left( {{p^2} + {q^2}} \right)\sin \theta }}{{p\cos \theta + q\sin \theta }}$$
View Solution
From Sine Rule
$$\eqalign{
& \frac{{{\text{AB}}}}{{\sin \theta }} = \frac{{\sqrt {{p^2} + {q^2}} }}{{\sin \left( {\pi - \left( {\theta + \alpha } \right)} \right)}} \cr
& {\text{AB}} = \frac{{\sqrt {{p^2} + {q^2}} \sin \theta }}{{\sin \theta \cos \alpha + \cos \theta \sin \alpha }} \cr
& = \frac{{\left( {{p^2} + {q^2}} \right)\sin \theta }}{{q\sin \theta + p\cos \theta }} \cr
& \left( {\because \,\,\cos \alpha = \frac{q}{{\sqrt {{p^2} + {q^2}} }}\,{\text{and sin}}\alpha = \frac{p}{{\sqrt {{p^2} + {q^2}} }}} \right) \cr} $$
116.
$${\sec ^2}\theta = \frac{{4xy}}{{{{\left( {x + y} \right)}^2}}}$$ is true if and only if
A
$$x + y \ne 0$$
B
$$x = y,x \ne 0$$
C
$$x = y$$
D
$$x \ne 0,y \ne 0$$
Answer :
$$x = y,x \ne 0$$
View Solution
We have $${\sec ^2}\theta = \frac{{4xy}}{{{{\left( {x + y} \right)}^2}}}$$
117.
What is the value of $$\left( {1 + \cos \frac{\pi }{8}} \right)\left( {1 + \cos \frac{{3\pi }}{8}} \right)\left( {1 + \cos \frac{{5\pi }}{8}} \right)\left( {1 + \cos \frac{{7\pi }}{8}} \right)?$$
A
$$\frac{1}{2}$$
B
$$\frac{1}{2} + \frac{1}{{2\sqrt 2 }}$$
C
$$\frac{1}{2} - \frac{1}{{2\sqrt 2 }}$$
D
$$\frac{1}{8}$$
Answer :
$$\frac{1}{8}$$
View Solution
$$\left[ {1 + \cos \frac{\pi }{8}} \right]\left[ {1 + \cos \frac{{3\pi }}{8}} \right]\left[ {1 + \cos \frac{{5\pi }}{8}} \right]\left[ {1 + \frac{{\cos 7\pi }}{8}} \right]$$
118.
If an angle $$B$$ is complement of an angle $$A,$$ what are the greatest and least values of $$\cos A \cos B$$ respectively ?
A
$$0, - \frac{1}{2}$$
B
$$\frac{1}{2}, - 1$$
C
$$1, 0$$
D
$$\frac{1}{2}, - \frac{1}{2}$$
Answer :
$$\frac{1}{2}, - \frac{1}{2}$$
View Solution
Since, $$A$$ and $$B$$ are complementary angles, then $$A + B = {90^ \circ }$$
119.
What is $$\frac{{\cos 7x - \cos 3x}}{{\sin 7x - 2\sin 5x + \sin 3x}}$$ equal to ?
A
$$\tan x$$
B
$$\cot x$$
C
$$\tan 2x$$
D
$$\cot 2x$$
Answer :
$$\cot x$$
View Solution
$$\eqalign{
& \frac{{\cos 7x - \cos 3x}}{{\sin 7x - 2\sin 5x + \sin 3x}} \cr
& = \frac{{ - 2\sin \frac{{7x + 3x}}{2} \cdot \sin \frac{{7x - 3x}}{2}}}{{2\sin \frac{{7x + 3x}}{2} \cdot \cos \frac{{7x - 3x}}{2} - 2\sin 5x}} \cr} $$
120.
If $$\frac{{\sin \left( {x + y} \right)}}{{\sin \left( {x - y} \right)}} = \frac{{a + b}}{{a - b}},$$ then what is $$\frac{{\tan x}}{{\tan y}}$$ equal to ?
A
$$\frac{b}{a}$$
B
$$\frac{a}{b}$$
C
$$ab$$
D
$$1$$
Answer :
$$\frac{a}{b}$$
View Solution
$$\frac{{\sin \left( {x + y} \right)}}{{\sin \left( {x - y} \right)}} = \frac{{a + b}}{{a - b}}$$