51.
If $${\cos ^4}\theta \cdot {\sec ^2}\alpha ,\frac{1}{2}$$ and $${\sin ^4}\theta \cdot {\text{cose}}{{\text{c}}^2}\alpha $$ are in A.P. then $${\cos ^8}\theta \cdot {\sec ^6}\alpha ,\frac{1}{2}$$ and $${\sin ^8}\theta \cdot {\text{cose}}{{\text{c}}^6}\alpha $$ are in
A
A.P.
B
G.P.
C
H.P.
D
None of these
Answer :
A.P.
View Solution
Here, $${\cos ^4}\theta \cdot {\sec ^2}\alpha + {\sin ^4}\theta \cdot {\text{cose}}{{\text{c}}^2}\alpha = 1$$
52.
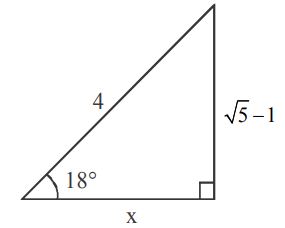
If $$\sin {18^ \circ } = \frac{{\sqrt 5 - 1}}{4} ,$$ then what is the value of $$\sin {81^ \circ } ?$$
A
$$\frac{{\sqrt {3 + \sqrt 5 } + \sqrt {5 - \sqrt 5 } }}{4}$$
B
$$\frac{{\sqrt {3 + \sqrt 5 } + \sqrt {5 + \sqrt 5 } }}{4}$$
C
$$\frac{{\sqrt {3 - \sqrt 5 } + \sqrt {5 - \sqrt 5 } }}{4}$$
D
$$\frac{{\sqrt {3 + \sqrt 5 } - \sqrt {5 - \sqrt 5 } }}{4}$$
Answer :
$$\frac{{\sqrt {3 + \sqrt 5 } + \sqrt {5 - \sqrt 5 } }}{4}$$
View Solution
$$\eqalign{
& \because \sin {18^ \circ } = \frac{{\sqrt 5 - 1}}{4} \cr
& {x^2} = {4^2} - {\left( {\sqrt 5 - 1} \right)^2} \cr
& \Rightarrow x = \sqrt {10 + 2\sqrt 5 } \cr
& \Rightarrow \cos {18^ \circ } = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4} \cr
& \Rightarrow 2{\cos ^2}9 - 1 = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4} \cr
& {\cos ^2}9 = \frac{{\sqrt {10 + 2\sqrt 5 } + 4}}{8} \cr
& \Rightarrow \,{\sin ^2}81 = \frac{{4 + \sqrt {10 + 2\sqrt 5 } }}{8} \cr} $$
After squaring all the options available, we come to a conclusion that option $$\left( A \right)$$ is correct.
53.
If $$\sin \theta = 3\sin \left( {\theta + 2\alpha } \right),$$ then the value of $$\tan\left( {\theta + \alpha } \right) + 2\tan \alpha $$ is
A
$$3$$
B
$$2$$
C
$$ - 1$$
D
$$0$$
Answer :
$$0$$
View Solution
$$\eqalign{
& \sin \theta = 3\sin \left( {\theta + 2\alpha } \right) \cr
& \Rightarrow \sin \left( {\theta + \alpha - \alpha } \right) = 3\sin \left( {\theta + \alpha + \alpha } \right) \cr
& \Rightarrow \sin \left( {\theta + \alpha } \right)\cos \alpha - \cos \left( {\theta + \alpha } \right)\sin \alpha = 3\sin \left( {\theta + \alpha } \right)\cos \alpha + 3\cos \left( {\theta + \alpha } \right)\sin \alpha \cr
& \Rightarrow - 2\sin \left( {\theta + \alpha } \right)\cos \alpha = 4\cos \left( {\theta + \alpha } \right)\sin \alpha \cr
& \Rightarrow \frac{{ - \sin \left( {\theta + \alpha } \right)}}{{\cos \left( {\theta + \alpha } \right)}} = \frac{{2\sin \alpha }}{{\cos \alpha }} \cr
& \Rightarrow \tan\left( {\theta + \alpha } \right) + 2\tan \alpha = 0 \cr} $$
54.
What is the angle (in circular measure) between the hour hand and the minute hand of a clock when the time is half past 4 ?
A
$$\frac{\pi }{3}$$
B
$$\frac{\pi }{4}$$
C
$$\frac{\pi }{6}$$
D
None of these
Answer :
$$\frac{\pi }{4}$$
View Solution
Angle traced by the hour hand in 12 hours $$ = {360^ \circ }$$
55.
If $$\alpha + \beta = \frac{\pi }{2}\,{\text{and }}\beta + \gamma = \alpha ,$$ then $$\tan \alpha $$ equals
A
$$2\left( {\tan \beta + \tan \gamma } \right)$$
B
$${\tan \beta + \tan \gamma }$$
C
$${\tan \beta + 2\tan \gamma }$$
D
$${2\tan \beta + \tan \gamma }$$
Answer :
$${\tan \beta + 2\tan \gamma }$$
View Solution
Given that $$\alpha + \beta = \frac{\pi }{2}\,$$
56.
$$\sin A + 2 \sin 2A + \sin 3A\,$$ is equal to which of the following ?
A
1 and 2 only
B
2 and 3 only
C
1 and 3 only
D
1, 2 and 3
Answer :
1 and 3 only
View Solution
$$\eqalign{
& {\text{Let}}\,A = {30^ \circ } \cr
& \Rightarrow \sin A + 2\sin 2A + \sin 3A \cr
& = \sin {30^ \circ } + 2\sin {60^ \circ } + \sin {90^ \circ } \cr
& = \frac{1}{2} + \frac{{2\sqrt 3 }}{2} + 1 = \frac{{2\sqrt 3 + 3}}{2}\left( {\because 2\,{{\cos }^2}A = 1 + \cos 2A} \right) \cr
& {\text{Now, }}4\sin 2A{\cos ^2}\left( {\frac{A}{2}} \right) = 2\sin 2A\left[ {1 + \cos A} \right] \cr
& = 2\sin {60^ \circ }\left[ {1 + \cos {{30}^ \circ }} \right] = \frac{{2\sqrt 3 + 3}}{2} \cr
& {\text{Also, }}\sin 2A = 2\sin A\cos A\,\,\& \,\,{\sin ^2}A + {\cos ^2}A = 1 \cr
& 2\sin 2A{\left[ {\sin \frac{A}{2} + \cos \frac{A}{2}} \right]^2} \cr
& = 2\sin 2A\left[ {{{\sin }^2}\frac{A}{2} + {{\cos }^2}\frac{A}{2} + 2\sin \frac{A}{2}\cos \frac{A}{2}} \right] \cr
& = 2\sin 2A\left[ {1 + \sin A} \right] = 2\sin {60^ \circ }\left[ {1 + \sin {{30}^ \circ }} \right] = \frac{{3\sqrt 3 }}{2} \cr
& \& \,\,8\sin A\cos A{\cos ^2}\left( {\frac{A}{2}} \right) \cr
& = 4\sin A\cos A\left[ {1 + \cos A} \right] \cr
& = 4\sin {30^ \circ }\cos {30^ \circ }\left[ {1 + \cos {{30}^ \circ }} \right] \cr
& = \frac{{2\sqrt 3 + 3}}{2} \cr} $$
57.
The value of $$\tan {20^ \circ } + 2\tan {50^ \circ } - \tan {70^ \circ }$$ is
A
$$1$$
B
$$0$$
C
$$\tan {50^ \circ }$$
D
None of these
Answer :
$$0$$
View Solution
Value $$ = 2\tan {50^ \circ } - \left( {\tan {{70}^ \circ } - \tan {{20}^ \circ }} \right)$$
58.
If $$0 < \phi < \frac{\pi }{2},x = \sum\limits_{n = 0}^\infty {{{\cos }^{2n}}\phi } ,y = \sum\limits_{n = 0}^\infty {{{\sin }^{2n}}\phi } $$ and $$z = \sum\limits_{n = 0}^\infty {{{\cos }^{2n}}\phi \cdot {{\sin }^{2n}}\phi } $$ then
A
$$xyz = xz + y$$
B
$$xyz = xy + z$$
C
$$xyz = x + y + z$$
D
$$xyz = yz + x$$
Answer :
$$xyz = xy + z$$
View Solution
$$\eqalign{
& x = 1 + {\cos ^2}\phi + {\cos ^4}\phi + .....\,{\text{to }}\infty = \frac{1}{{1 - {{\cos }^2}\phi }} = \frac{1}{{{{\sin }^2}\phi }}. \cr
& {\text{Similarly, }}y = \frac{1}{{1 - {{\sin }^2}\phi }} = \frac{1}{{{{\cos }^2}\phi }},z = \frac{1}{{1 - {{\cos }^2}\phi \cdot {{\sin }^2}\phi }} \cr
& \therefore \,\,xyz = \frac{1}{{{{\sin }^2}\phi \cdot {{\cos }^2}\phi \left( {1 - {{\sin }^2}\phi \,{{\cos }^2}\phi } \right)}} \cr
& xyz = \frac{{\left( {1 - {{\sin }^2}\phi \cdot {{\cos }^2}\phi } \right) + {{\sin }^2}\phi \cdot {{\cos }^2}\phi }}{{{{\sin }^2}\phi \cdot {{\cos }^2}\phi \left( {1 - {{\sin }^2}\phi \,{{\cos }^2}\phi } \right)}} \cr
& xyz = \frac{1}{{{{\sin }^2}\phi \,{{\cos }^2}\phi }} + \frac{1}{{1 - {{\sin }^2}\phi \,{{\cos }^2}\phi }} = xy + z. \cr} $$
59.
If $$\tan \theta = - \frac{4}{3},$$ then $$\sin \theta $$ is
A
$$ - \frac{4}{5}{\text{ but not }}\frac{4}{5}$$
B
$$ - \frac{4}{5}{\text{ or }}\frac{4}{5}$$
C
$$ \frac{4}{5}{\text{ but not }} - \frac{4}{5}$$
D
None of these
Answer :
$$ - \frac{4}{5}{\text{ or }}\frac{4}{5}$$
View Solution
$$\tan \theta = - \frac{4}{3}$$
60.
A line makes the same angle $$\theta ,$$ with each of the $$x$$ and $$z$$ - axis. If the angle $$\beta ,$$ which it makes with $$y$$ - axis, is such that $${\sin ^2}\beta = 3{\sin ^2}\theta ,$$ then $${\cos ^2}\theta $$ equals
A
$$\frac{2}{5}$$
B
$$\frac{1}{5}$$
C
$$\frac{3}{5}$$
D
$$\frac{2}{3}$$
Answer :
$$\frac{3}{5}$$
View Solution
The direction cosines of the line are $$\cos \theta ,\cos \beta ,\cos \theta $$