101. The number of complex numbers $$z$$ such that $$\left| {z - 1} \right| = \left| {z + 1} \right| = \left| {z - i} \right|$$ equals
A
$$1$$
B
$$2$$
C
$$\infty $$
D
$$0$$
Answer :
$$1$$
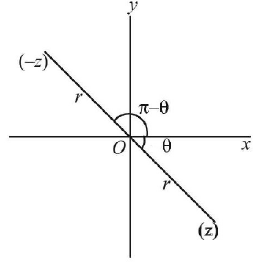
102. If $${\text{arg}}\left( z \right) < 0,{\text{then arg}}\left( { - z} \right) - {\text{arg}}\left( z \right) = $$
A
$$\pi $$
B
$$ - \pi $$
C
$$ - \frac{\pi }{2}$$
D
$$\frac{\pi }{2}$$
Answer :
$$\pi $$
103. If $$z$$ and $$\omega $$ are two non-zero complex numbers such that $$\left| {z\omega } \right| = 1{\text{ and Arg}}\left( z \right) - {\text{Arg}}\left( \omega \right) = \frac{\pi }{2},{\text{then }}\overline z \omega $$ is equal to
A
$$ - i$$
B
$$1$$
C
$$ - 1$$
D
$$i$$
Answer :
$$ - 1$$
104. All the points in the set $$S = \left\{ {\frac{{\alpha + i}}{{\alpha - i}}:\alpha \in R} \right\}\left( {i = \sqrt { - 1} } \right)$$ lie on a :
A
straight line whose slope is 1.
B
circle whose radius is 1.
C
circle whose radius is $$\sqrt 2 .$$
D
straight line whose slope is $$- 1.$$
Answer :
circle whose radius is 1.
105. If $$\left| {z - i} \right| \leqslant 2$$ and $${z_0} = 5 + 3i$$ then the maximum value of $$\left| {iz + {z_0}} \right|$$ is
A
$$2 + \sqrt {31} $$
B
$$7$$
C
$$ \sqrt {31} - 2 $$
D
None of these
Answer :
$$7$$
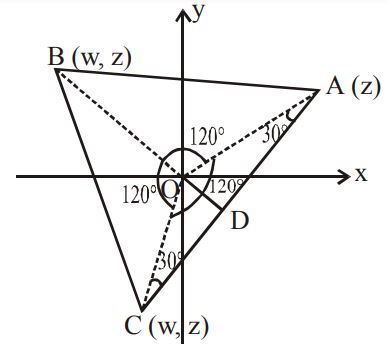
106. If $$z,\omega z$$ and $$\bar \omega z$$ are the vertices of a triangle, then the area of the triangle will be (where $$\omega$$ is cube root of unity) :
A
$$\frac{{3{{\left| z \right|}^2}}}{2}$$
B
$$\frac{{3 \sqrt 3 {{\left| z \right|}^2}}}{2}$$
C
$$\frac{{ \sqrt 3 {{\left| z \right|}^2}}}{2}$$
D
None of these
Answer :
$$\frac{{3 \sqrt 3 {{\left| z \right|}^2}}}{2}$$
107. A particle $$P$$ starts from the point $${z_0} = 1 + 2i,$$ where $$i = \sqrt { - 1} .$$ It moves horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point $${z_1}.$$ From $${z_1}$$ the particle moves $$\sqrt 2 $$ units in the direction of the vector $$\hat i + \hat j$$ and then it moves through an angle $$\frac{\pi }{2}$$ in anticlockwise direction on a circle with center at origin, to reach a point $${z_2}.$$ The point $${z_2}$$ is given by
A
$$6 + 7i$$
B
$$- 7 + 6i$$
C
$$7 + 6i$$
D
$$- 6 + 7i$$
Answer :
$$- 6 + 7i$$
108. Let $${z_1} = a + ib,{z_2} = p + iq$$ be two unimodular complex numbers such that $$\operatorname{Im} \left( {{z_1}{{\overline z }_2}} \right) = 1.$$ If $${\omega _1} = a + ip,{\omega _2} = b + iq$$ then
A
$$\operatorname{Re} \left( {{\omega _1}{\omega _2}} \right) = 1$$
B
$$\operatorname{Im} \left( {{\omega _1}{\omega _2}} \right) = 1$$
C
$$\operatorname{Re} \left( {{\omega _1}{\omega _2}} \right) = 0$$
D
$$\operatorname{Im} \left( {{\omega _1}{{\overline \omega }_2}} \right) = 1$$
Answer :
$$\operatorname{Im} \left( {{\omega _1}{{\overline \omega }_2}} \right) = 1$$
109. For positive integers $${n_1},{n_2}$$ the value of the expression $${\left( {1 + i} \right)^{{n_1}}} + {\left( {1 + {i^3}} \right)^{{n_1}}} + {\left( {1 + {i^5}} \right)^{{n_2}}} + {\left( {1 + {i^7}} \right)^{{n_2}}},$$ where $$i = \sqrt { - 1} $$ is a real number if and only if
A
$${n_1} = {n_2} + 1$$
B
$${n_1} = {n_2} - 1$$
C
$${n_1} = {n_2}$$
D
$${n_1} > 0,{n_2} > 0$$
Answer :
$${n_1} > 0,{n_2} > 0$$
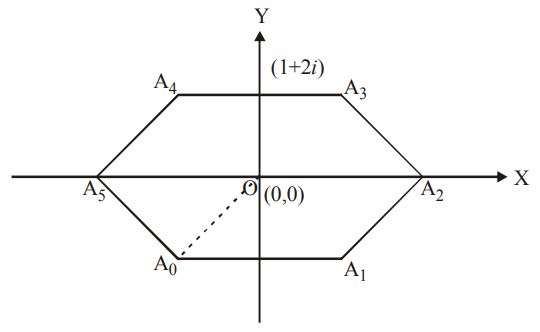
110. If center of a regular hexagon is at origin and one of the vertex on argand diagram is $$1 + 2i,$$ then its perimeter is
A
$$2\sqrt 5 $$
B
$$6\sqrt 2 $$
C
$$4\sqrt 5 $$
D
$$6\sqrt 5 $$
Answer :
$$6\sqrt 5 $$