101.
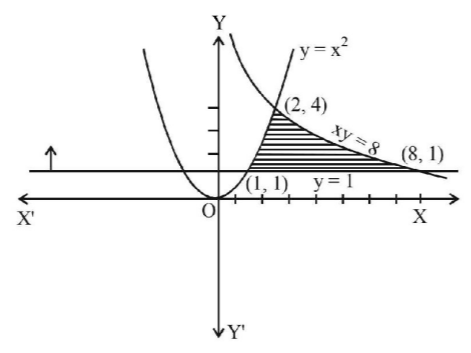
The area of the region $$\left\{ {x,\,y\,:\,xy \leqslant 8,\,1 \leqslant y \leqslant {x^2}} \right\}$$ is-
A
$$8\,{\log _e}2 - \frac{{14}}{3}$$
B
$$16\,{\log _e}2 - \frac{{14}}{3}$$
C
$$8\,{\log _e}2 - \frac{7}{3}$$
D
$$16\,{\log _e}2 - 6$$
Answer :
$$16\,{\log _e}2 - \frac{{14}}{3}$$
View Solution
$$xy \leqslant 8,\,\,1 \leqslant y \leqslant {x^2}$$
Intersection points of $$xy= 8$$ and $$y= 1$$ is $$\left( {8,\,1} \right);xy = 8$$ and $$y = {x^2}$$ is $$\left( {2,\,4} \right)$$ and $$y = {x^2}$$ and $$y =1$$ is $$\left( {1,\,1} \right)$$
$$\eqalign{
& {\text{Required area}}\, = \int\limits_1^2 {{x^2}dx} + \int\limits_2^8 {\frac{8}{x}dx} - \int\limits_1^8 {1\,dx} \cr
& = \left( {\frac{{{x^3}}}{3}} \right)_1^2 + \left( {8\ln \,x} \right)_2^8 - \left( x \right)_1^8 \cr
& = \frac{8}{3} - \frac{1}{3} + 8\,\ln \,8 - 8\,\ln \,2 - \left( {8 - 1} \right) \cr
& = \frac{7}{3} + 24\,\ln \,2 - 8\,\ln \,2 - 7 \cr
& = 16\,\ln \,2 - \frac{{14}}{3} \cr
& \therefore {\text{ Correct option is (B)}} \cr} $$
102.
The area bounded by the curve $$y = x{\left( {3 - x} \right)^2},$$ the
$$x$$-axis and the ordinates of the maximum and minimum points of the curve, is given by :
A
1 sq. unit
B
2 sq. units
C
4 sq. units
D
None of these
Answer :
4 sq. units
View Solution
Clearly, the curve $$y = x{\left( {3 - x} \right)^2},$$ has
maximum at $$x = 1$$ and minimum at $$x = 3$$
$$\therefore $$ Required area
$$\eqalign{
& = \int_1^3 {x{{\left( {3 - x} \right)}^2}dx} \cr
& = \int_1^3 {\left( {{x^3} - 6{x^2} + 9x} \right)\,dx} \cr
& = \left[ {\frac{{{x^4}}}{4} - 2{x^3} + \frac{{9{x^2}}}{2}} \right]_1^3 \cr
& = 4{\text{ sq}}{\text{. units}} \cr} $$
103.
Let $$f$$ be a positive function. If $${I_1} = \int_{1 - k}^k {xf\left\{ {x\left( {1 - x} \right)} \right\}dx,\,{I_2}} = \int_{1 - k}^k {f\left\{ {x\left( {1 - x} \right)} \right\}dx,} $$ where $$2k - 1 > 0,$$ then $$\frac{{{I_1}}}{{{I_2}}}$$ is :
A
2
B
$$k$$
C
$$\frac{1}{2}$$
D
1
Answer :
$$\frac{1}{2}$$
View Solution
$$\eqalign{
& {I_1} = \int_{1 - k}^k {xf\left\{ {x\left( {1 - x} \right)} \right\}dx} \cr
& {\text{Put }}x = 1 - z \cr
& {I_1} = \int_k^{1 - k} {\left( {1 - z} \right)f\left\{ {\left( {1 - z} \right)z} \right\}d\left( {1 - z} \right)} \cr
& \,\,\,\,\, = \int_{1 - k}^k {f\left\{ {z\left( {1 - z} \right)} \right\}dz} - \int_{1 - k}^k {zf\left\{ {z\left( {1 - z} \right)} \right\}dz} \cr
& \,\,\,\,\, = {I_2} - {I_1} \cr
& \therefore 2{I_1} = {I_2} \cr} $$
104.
$$\int_{ - 1}^1 {\left( {x - \left[ {2x} \right]} \right)dx} $$ is equal to :
A
1
B
0
C
2
D
4
Answer :
1
View Solution
$$\eqalign{
& I = \int_{ - 1}^1 {x\,dx} - \int_{ - 1}^1 {\left[ {2x} \right]dx} \cr
& \,\,\,\,\, = \left[ {\frac{{{x^2}}}{2}} \right]_{ - 1}^1 - \left\{ {\int_{ - 1}^{ - \frac{1}{2}} {\left[ {2x} \right]dx} + \int_{ - \frac{1}{2}}^0 {\left[ {2x} \right]dx} + \int_0^{\frac{1}{2}} {\left[ {2x} \right]dx} + \int_{\frac{1}{2}}^1 {\left[ {2x} \right]dx} } \right\} \cr
& \,\,\,\,\, = 0 - \left\{ {\int_{ - 1}^{ - \frac{1}{2}} { - 2\,dx} + \int_{ - \frac{1}{2}}^0 { - 1\,dx} + \int_0^{\frac{1}{2}} {0\,dx} + \int_{\frac{1}{2}}^1 {1\,dx} } \right\} \cr
& \,\,\,\,\, = 2\left[ x \right]_{ - 1}^{ - \frac{1}{2}} - \left[ x \right]_{ - \frac{1}{2}}^0 - \left[ x \right]_{ - \frac{1}{2}}^1 \cr
& \,\,\,\,\, = 2\left( { - \frac{1}{2} + 1} \right) + \left( {0 + \frac{1}{2}} \right) - \left( {1 - \frac{1}{2}} \right) \cr
& \,\,\,\,\, = 1 \cr} $$
105.
The area of the region between the curves $$y = \sqrt {\frac{{1 + \sin \,x}}{{\cos \,x}}} $$ and $$y = \sqrt {\frac{{1 - \sin \,x}}{{\cos \,x}}} $$ bounded by the lines $$x = 0$$ and $$x = \frac{\pi }{4}$$ is-
A
$$\int\limits_0^{\sqrt 2 - 1} {\frac{t}{{\left( {1 + {t^2}} \right)\sqrt {1 - {t^2}} }}dt} $$
B
$$\int\limits_0^{\sqrt 2 - 1} {\frac{{4t}}{{\left( {1 + {t^2}} \right)\sqrt {1 - {t^2}} }}dt} $$
C
$$\int\limits_0^{\sqrt 2 + 1} {\frac{{4t}}{{\left( {1 + {t^2}} \right)\sqrt {1 - {t^2}} }}dt} $$
D
$$\int\limits_0^{\sqrt 2 + 1} {\frac{t}{{\left( {1 + {t^2}} \right)\sqrt {1 - {t^2}} }}dt} $$
Answer :
$$\int\limits_0^{\sqrt 2 - 1} {\frac{{4t}}{{\left( {1 + {t^2}} \right)\sqrt {1 - {t^2}} }}dt} $$
View Solution
The given curves are
106.
The area of the region bounded by the pairs of lines $$y = \left| {x - 1} \right|$$ and $$y = 3 - \left| x \right|$$ is :
A
$$3\,{\text{uni}}{{\text{t}}^2}$$
B
$$4\,{\text{uni}}{{\text{t}}^2}$$
C
$$6\,{\text{uni}}{{\text{t}}^2}$$
D
$$2\,{\text{uni}}{{\text{t}}^2}$$
Answer :
$$4\,{\text{uni}}{{\text{t}}^2}$$
View Solution
$${\text{Area}} = \sqrt 2 \times 2\sqrt 2 $$
107.
If $$y = \int_0^x {\sqrt {\sin \,x} \,dx} $$ then the value of $$\frac{{dy}}{{dx}}$$ at $$x = \frac{\pi }{2}$$ is :
A
0
B
1
C
$$-1$$
D
none of these
Answer :
1
View Solution
$$\frac{{dy}}{{dx}} = \sqrt {\sin \,x} \,\,\,\,\,\,\,\,\,\,\therefore {\left. {\frac{{dy}}{{dx}}} \right)_{x = \frac{\pi }{2}}} = 1$$
108.
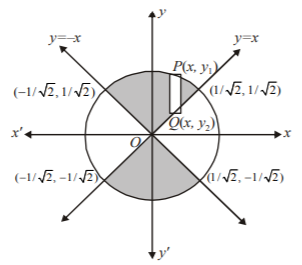
The area of the region $$R = \left\{ {\left( {x,\,y} \right):\left| x \right| \leqslant \left| y \right|{\text{ and }}{x^2} + {y^2} \leqslant 1} \right\}$$ is :
A
$$\frac{{3\pi }}{8}{\text{ sq}}{\text{. unit}}$$
B
$$\frac{{5\pi }}{8}{\text{ sq}}{\text{. unit}}$$
C
$$\frac{\pi }{2}{\text{ sq}}{\text{. unit}}$$
D
$$\frac{\pi }{8}{\text{ sq}}{\text{. unit}}$$
Answer :
$$\frac{\pi }{2}{\text{ sq}}{\text{. unit}}$$
View Solution
Required area $$=$$ area of the shaded region
$$ = 4$$ (area of the shaded region in first quadrant
$$\eqalign{
& = 4\int_0^{\frac{1}{{\sqrt 2 }}} {\left( {{y_1} - {y_2}} \right)} dx \cr
& = 4\int_0^{\frac{1}{{\sqrt 2 }}} {\left( {\sqrt {1 - {x^2}} - x} \right)dx} \cr
& = 4\left[ {\frac{1}{2} \times \sqrt {1 - {x^2}} + \frac{1}{2}{{\sin }^{ - 1}}x - \frac{{{x^2}}}{2}} \right]_0^{\frac{1}{{\sqrt 2 }}} \cr
& = \frac{\pi }{2}{\text{ sq}}{\text{. unit}} \cr} $$
109.
If $$y = \int_x^{{x^2}} {\sqrt {5 - {t^2}} dt} $$ then the value of $$\frac{{dy}}{{dx}}$$ at $$x = \sqrt 2 $$ is :
A
$$1 - \sqrt 3 $$
B
$$\sqrt 3 \left( {2\sqrt 6 - 1} \right)$$
C
$$2\sqrt 2 - \sqrt 3 $$
D
none of these
Answer :
$$2\sqrt 2 - \sqrt 3 $$
View Solution
$$\eqalign{
& y = \int_x^{{x^2}} {\sqrt {5 - {t^2}} dt} - \int_0^x {\sqrt {5 - {t^2}} dt} \cr
& {\text{Differentiating w}}{\text{.r}}{\text{.t}}{\text{. }}x, \cr
& \frac{{dy}}{{dx}} = \sqrt {5 - {{\left( {{x^2}} \right)}^2}} .2x - \sqrt {5 - {x^2}} \cr
& {\text{Put }}x = \sqrt 2 \cr} $$
110.
Let $$f$$ and $$g$$ be two continuous functions. Then $$\int_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\left\{ {f\left( x \right) + f\left( { - x} \right)} \right\}\left\{ {g\left( x \right) - g\left( { - x} \right)} \right\}} dx$$ is equal to :
A
$$\pi $$
B
1
C
$$-1$$
D
0
Answer :
0
View Solution
Clearly, $$f\left( x \right) + f\left( { - x} \right)$$ is an even function while $$g\left( x \right) - g\left( { - x} \right)$$ is an odd
function.