51.
Let $$\int_a^b {f\left( x \right)dx = p} $$ and $$\int_a^b {\left| {f\left( x \right)} \right|dx = q.} $$ Then :
A
$$\left| p \right| \leqslant q$$
B
$$p > q$$
C
$$p + q = 0$$
D
none of these
Answer :
$$\left| p \right| \leqslant q$$
View Solution
Use the property $$\left| {\int_a^b {f\left( x \right)dx} } \right| \leqslant \int_a^b {\left| {f\left( x \right)} \right|dx.} $$
52.
If $$I = \int_0^1 {\frac{{x\,dx}}{{8 + {x^3}}}} $$ then the smallest interval in which $$I$$ lies is
A
$$\left( {0,\,\frac{1}{8}} \right)$$
B
$$\left( {0,\,\frac{1}{9}} \right)$$
C
$$\left( {0,\,\frac{1}{{10}}} \right)$$
D
$$\left( {0,\,\frac{1}{7}} \right)$$
Answer :
$$\left( {0,\,\frac{1}{9}} \right)$$
View Solution
$$\eqalign{
& {\text{Let }}f\left( x \right) = \frac{x}{{8 + {x^3}}} \cr
& {\text{Then }}f'\left( x \right) = \frac{{1.\left( {8 + {x^3}} \right) - x\left( {3{x^2}} \right)}}{{{{\left( {8 + {x^3}} \right)}^2}}} = \frac{{8 - 2{x^3}}}{{{{\left( {8 + {x^3}} \right)}^2}}} > 0{\text{ for }}x\, \in \left[ {0,\,1} \right] \cr
& \therefore f\left( x \right)\,{\text{is m}}{\text{.i}}{\text{. in }}\left[ {0,\,1} \right].{\text{ So, }}f\left( 0 \right) \leqslant f\left( x \right) \leqslant f\left( 1 \right) \cr
& \therefore 0 \leqslant f\left( x \right) \leqslant \frac{1}{{8 + 1}} \cr
& \therefore \int_0^1 {0\,dx < } \int_0^1 {f\left( x \right)} dx < \frac{1}{9}\int_0^1 {1\,dx} \cr
& \therefore 0 < \int_0^1 {f\left( x \right)} dx < \frac{1}{9} \cr} $$
53.
If $$\left[ x \right]$$ denotes the greatest integer less than or equal to $$x$$ then $$\int_0^\infty {\left[ {\frac{2}{{{e^x}}}} \right]dx} $$ is equal to :
A
$${\log _e}2$$
B
$${e^2}$$
C
0
D
$$\frac{2}{e}$$
Answer :
$${\log _e}2$$
View Solution
$$\eqalign{
& I = \int_0^\infty {\left[ {\frac{2}{{{e^x}}}} \right]dx} \cr
& {\text{Substitute }}{e^x} = t \Rightarrow x = \log \,t \cr
& dx = \frac{1}{t}dt \cr
& {\text{Then}} \cr
& I = \int_1^\infty {\left[ {\frac{2}{t}} \right]\frac{{dt}}{t}} \cr
& = \int_1^2 {\left[ { - \frac{2}{t}} \right]\frac{{dt}}{t}} + \int_2^\infty {\left[ {\frac{2}{t}} \right]\frac{{dt}}{t}} \cr
& = \int_1^2 {\frac{{dt}}{t}} + \int_2^\infty {0.} \frac{{dt}}{t} \cr
& = \left[ {\log \,t} \right]_1^2 \cr
& = \log \,2 - \log \,1 \cr
& = \log \,2 - 0 \cr
& = \log \,2 \cr
& = {\log _e}2 \cr
& \therefore \,I = {\log _e}2 \cr} $$
54.
The area enclosed between the curves $$y = a{x^2}$$ and $$x = a{y^2}\left( {a > 0} \right)$$ is 1 sq. unit, then the value of $$a$$ is-
A
$$\frac{1}{{\sqrt 3 }}$$
B
$$\frac{1}{2}$$
C
$$1$$
D
$$\frac{1}{3}$$
Answer :
$$\frac{1}{{\sqrt 3 }}$$
View Solution
$$y = a{x^2}{\text{ and }}x = a{y^2}$$
55.
If $$y = f\left( x \right)$$ makes $$+ve$$ intercept of $$2$$ and $$0$$ unit on $$x$$ and $$y$$ axes and encloses an area of $$\frac{3}{4}$$ square unit with the axes then $$\int\limits_0^2 {x\,f'\left( x \right)dx} $$ is :
A
$$\frac{3}{2}$$
B
$$1$$
C
$$\frac{5}{4}$$
D
$$ - \frac{3}{4}$$
Answer :
$$ - \frac{3}{4}$$
View Solution
We have $$\int\limits_0^2 {f\left( x \right)dx} = \frac{3}{4}\,;$$
56.
What is the area bounded by the curves $$y = {e^x},\,y = {e^{ - x}}$$ and the straight line $$x = 1\,?$$
A
$$\left( {e + \frac{1}{e}} \right)\,{\text{square}}\,{\text{unit}}$$
B
$$\left( {e - \frac{1}{e}} \right)\,{\text{square}}\,{\text{unit}}$$
C
$$\left( {e + \frac{1}{e} - 2} \right)\,{\text{square}}\,{\text{unit}}$$
D
$$\left( {e - \frac{1}{e} - 2} \right)\,{\text{square}}\,{\text{unit}}$$
Answer :
$$\left( {e + \frac{1}{e} - 2} \right)\,{\text{square}}\,{\text{unit}}$$
View Solution
Given equations of curves are $$y = {e^x}{\text{ and }}y = {e^{ - x}}$$
57.
The area bounded by the curve $$y = \sqrt {4 - {x^2}} $$ and the line $$y=0$$ is :
A
$$4\pi $$
B
$$2\pi $$
C
$$\pi $$
D
$$\frac{\pi }{2}$$
Answer :
$$2\pi $$
View Solution
Area $$=$$ area of the semicircle of radius 2
58.
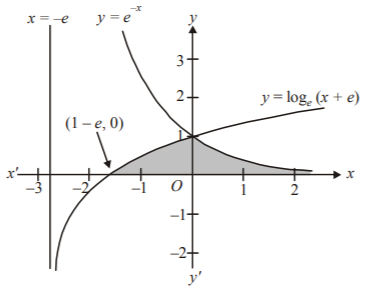
The area enclosed between the curves $$y = {\log _e}\left( {x + e} \right),\,x = {\log _e}\left( {\frac{1}{y}} \right),$$ and the $$x$$-axis is :
A
2 sq. units
B
1 sq. unit
C
4 sq. units
D
None of these
Answer :
2 sq. units
View Solution
$$y = {\log _e}\left( {x + e} \right),\,x = {\log _e}\left( {\frac{1}{y}} \right),{\text{ or }}y = {e^{ - x}}$$
For $$y = {\log _e}\left( {x + e} \right),$$ shift the graph of $$y = {\log _e}x,\,\,e$$ units to the left hand side.
Required area
$$\eqalign{
& = \int\limits_{1 - e}^0 {{{\log }_e}\left( {x + e} \right)} dx + \int\limits_0^\infty {{e^{ - x}}dx} \cr
& = \left| {x\,{{\log }_e}\left( {x + e} \right)} \right|_{1 - e}^0 - \int\limits_{1 - e}^0 {\frac{x}{{x + e}}} dx - \left| {{e^{ - x}}} \right|_0^\infty \cr
& = \int\limits_0^{1 - e} {\left( {1 - \frac{e}{{x + e}}} \right)dx - {e^{ - \infty }}} + {e^0} \cr
& = \left| {x - e\,\log \left( {x + e} \right)} \right|_0^{1 - e} - 0 + 1 \cr
& = 1 - e + e\,\log \,e + 1 \cr
& = 2{\text{ sq}}{\text{. units}} \cr} $$
59.
$$\int_{\frac{a}{4}}^{\frac{{3a}}{4}} {\frac{{\sqrt x }}{{\sqrt {a - x} + \sqrt x }}} dx$$ is equal to :
A
$$\frac{a}{2}$$
B
$$a$$
C
$$-a$$
D
none of these
Answer :
$$\frac{a}{2}$$
View Solution
$$\eqalign{
& {\text{Put }}a - x = z \cr
& {\text{Then }}I = \int_{\frac{{3a}}{4}}^{\frac{a}{4}} {\frac{{\sqrt {a - z} }}{{\sqrt z + \sqrt {a - z} }}\left( { - dz} \right)} = \int_{\frac{a}{4}}^{\frac{{3a}}{4}} {\frac{{\sqrt {a - x} }}{{\sqrt x + \sqrt {a - x} }}dx} \cr
& \therefore I + I = \int_{\frac{a}{4}}^{\frac{{3a}}{4}} {\frac{{\sqrt x }}{{\sqrt {a - x} + \sqrt x }}dx} + \int_{\frac{a}{4}}^{\frac{{3a}}{4}} {\frac{{\sqrt {a - x} }}{{\sqrt x + \sqrt {a - x} }}dx} \cr
& = \int_{\frac{a}{4}}^{\frac{{3a}}{4}} {dx} \cr
& = \frac{{3a}}{4} - \frac{a}{4} \cr
& = \frac{a}{2} \cr} $$
60.
The area bounded by the curve $${x^2} = ky,\,k > 0$$ and the line $$y=3$$ is $$12\,{\text{uni}}{{\text{t}}^2}.$$ Then $$k$$ is :
A
3
B
$$3\sqrt 3 $$
C
$$\frac{3}{4}$$
D
none of these
Answer :
3
View Solution
$$\eqalign{
& {\text{Area}} = 2\int_0^3 {x\,dy} \cr
& = 2\int_0^3 {\sqrt {ky} } \,dy \cr
& = \left[ {2\sqrt k .\frac{{{y^{\frac{3}{2}}}}}{{\frac{3}{2}}}} \right]_0^3 \cr
& = \frac{{4\sqrt k }}{3}.3\sqrt 3 \cr
& \therefore 12 = 4\sqrt k .\sqrt 3 \,\,\,\,\, \Rightarrow k = 3 \cr} $$