1. If $$\left| z \right| = \max \left\{ {\left| {z - 1} \right|,\left| {z + 1} \right|} \right\}$$ then
A
$$\left| {z + \overline z } \right| = \frac{1}{2}$$
B
$$ {z + \overline z } = 1$$
C
$$\left| {z + \overline z } \right| = 1$$
D
None of these
Answer :
$$\left| {z + \overline z } \right| = 1$$
2.
If $${z^2} + z + 1 = 0,$$ where $$z$$ is complex number, then the value of
$${\left( {z + \frac{1}{z}} \right)^2} + {\left( {{z^2} + \frac{1}{{{z^2}}}} \right)^2} + {\left( {{z^3} + \frac{1}{{{z^3}}}} \right)^2} + ...... + \left( {{z^6} + \frac{1}{{{z^6}}}} \right)\,{\text{is}}$$
A
18
B
54
C
6
D
12
Answer :
12
3. If $$m_1 , m_2 , m_3$$ and $$m_4$$ respectively denote the moduli of the complex numbers $$1 + 4i, 3 + i, 1 – i$$ and $$2 – 3i,$$ then the correct one, among the following is
A
$${m_1} < {m_2} < {m_3} < {m_4}$$
B
$${m_4} < {m_3} < {m_2} < {m_1}$$
C
$${m_3} < {m_2} < {m_4} < {m_1}$$
D
$${m_3} < {m_1} < {m_2} < {m_4}$$
Answer :
$${m_3} < {m_2} < {m_4} < {m_1}$$
4. $$z$$ and $$w$$ are two nonzero complex numbers such that $$\left| z \right| = \left| w \right|\,\,{\text{and Arg}}\,z + {\text{Agr}}\,w = \pi $$ then $$z$$ equals
A
$$\overline \omega $$
B
$$ - \overline \omega $$
C
$$\omega $$
D
$$ - \omega $$
Answer :
$$ - \overline \omega $$
5. If $${z_1}\,{\text{and }}{z_2}$$ are two non- zero complex numbers such that $$\left| {{z_1} + {z_2}} \right| = \left| {{z_1}} \right| + \left| {{z_2}} \right|,{\text{then arg }}{z_1} - {\text{arg }}{z_2}$$ is equal to
A
$$\frac{\pi }{2}$$
B
$$ - \pi $$
C
$$0$$
D
$$ \frac{ - \pi }{2}$$
Answer :
$$0$$
6. If $$\operatorname{Re} \left( {\frac{{z - 1}}{{z + 1}}} \right) = 0,$$ where $$2 = x + iy$$ is a complex number, then which one of the following is correct ?
A
$$z = 1 + i$$
B
$$\left| z \right| = 2$$
C
$$z = 1 - i$$
D
$$\left| z \right| = 1$$
Answer :
$$\left| z \right| = 1$$
7. If $$z = x + iy\,\,{\text{and }}\omega = \frac{{\left( {1 - iz} \right)}}{{\left( {z - i} \right)}},{\text{then }}\left| \omega \right| = 1$$ implies that, in the complex plane,
A
$$z$$ lies on the imaginary axis
B
$$z$$ lies on the real axis
C
$$z$$ lies on the unit circle
D
None of these
Answer :
$$z$$ lies on the real axis
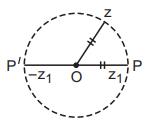
8. If $$P,P'$$ represent the complex number $${z_1}$$ and its additive inverse respectively then the complex equation of the circle with $$PP'$$ as a diameter is
A
$$\frac{z}{{{z_1}}} = \left( {\frac{{{{\overline z }_1}}}{z}} \right)$$
B
$$z\overline z + {z_1}{\overline z _1} = 0$$
C
$$z{\overline z _1} + \overline z {z_1} = 0$$
D
None of these
Answer :
$$\frac{z}{{{z_1}}} = \left( {\frac{{{{\overline z }_1}}}{z}} \right)$$
9. If $$f\left( z \right) = \frac{{7 - z}}{{1 - {z^2}}} ,$$ where $$z = 1 + 2i,$$ then $$\left| {f\left( z \right)} \right|$$ is equal to :
A
$$\frac{{\left| z \right|}}{2}$$
B
$${\left| z \right|}$$
C
$$2{\left| z \right|}$$
D
None of these
Answer :
$$\frac{{\left| z \right|}}{2}$$
10. If $${z_1},{z_2}$$ are two non-zero complex numbers such that $$\left| {{z_1} + {z_2}} \right| = \left| {{z_1}} \right| + \left| {{z_2}} \right|$$ then $${\text{amp}}\frac{{{z_1}}}{{{z_2}}}$$ is equal to
A
$$\pi $$
B
$$ - \pi $$
C
$$0$$
D
$$\frac{\pi }{2}$$
Answer :
$$0$$