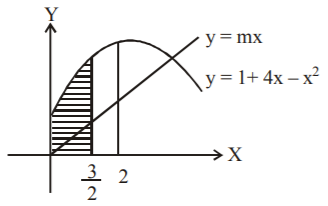131.
What is the area of the portion of the curve $$y = \sin \,x,$$ lying between $$x = 0,\,y = 0$$ and $$x = 2\pi \,?$$
A
1 square unit
B
2 square units
C
4 square units
D
8 square units
Answer :
2 square units
View Solution
Required area
132.
The line $$y = mx$$ bisects the area enclosed by lines $$x = 0,\,y = 0$$ and $$x = \frac{3}{2}$$ and the curve $$y = 1 + 4x - {x^2}.$$ Then the value of $$m$$ is :
A
$$\frac{{13}}{6}$$
B
$$\frac{{13}}{2}$$
C
$$\frac{{13}}{5}$$
D
$$\frac{{13}}{7}$$
Answer :
$$\frac{{13}}{6}$$
View Solution
$$y = 1 + 4x - {x^2} = 5 - {\left( {x - 2} \right)^2}$$
We have $$\int\limits_0^{\frac{3}{2}} {\left( {1 + 4x - {x^2}} \right)} dx$$
$$\eqalign{
& = 2\int\limits_0^{\frac{3}{2}} {mx\,dx} \cr
& = \frac{3}{2} + 2\left( {\frac{9}{4}} \right) - \frac{1}{3}\left( {\frac{{27}}{8}} \right) \cr
& = m.\frac{9}{4} \cr} $$
On solving we get $$m = \frac{{13}}{6}$$
133.
The triangle formed by the tangent to the curve $$f\left( x \right) = {x^2} + bx - b$$ at the point $$\left( {1,\,1} \right)$$ and the coordinate axes, lies in the first quadrant. If its area is $$2,$$ then the value of $$b$$ is :
A
$$ - 1$$
B
$$3$$
C
$$ - 3$$
D
$$1$$
Answer :
$$ - 3$$
View Solution
$$f\left( x \right) = {x^2} + bx - b\,;\,f'\left( x \right) = 2x + b\, \Rightarrow f'\left( 1 \right) = b + 2$$
134.
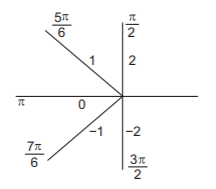
If $$\left[ y \right] = $$ the greatest integer less than or equal to $$y$$ then $$\int_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left[ {2\sin \,x} \right]dx} $$ is :
A
$$ - \pi $$
B
0
C
$$ - \frac{\pi }{2}$$
D
$$\frac{\pi }{2}$$
Answer :
$$ - \frac{\pi }{2}$$
View Solution
$$\eqalign{
& I = \int_{\frac{\pi }{2}}^{\frac{{5\pi }}{6}} {\left[ {2\sin \,x} \right]dx} + \int_{\frac{{5\pi }}{6}}^\pi {\left[ {2\sin \,x} \right]dx} + \int_\pi ^{\frac{{7\pi }}{6}} {\left[ {2\sin \,x} \right]dx} + \int_{\frac{{7\pi }}{6}}^{\frac{{3\pi }}{2}} {\left[ {2\sin \,x} \right]dx} \cr
& \,\,\,\,\, = \int_{\frac{\pi }{2}}^{\frac{{5\pi }}{6}} {1\,dx} + \int_{\frac{{5\pi }}{6}}^\pi {0\,dx} + \int_\pi ^{\frac{{7\pi }}{6}} { - 1\,dx} + \int_{\frac{{7\pi }}{6}}^{\frac{{3\pi }}{2}} { - 2\,dx} \cr
& \,\,\,\,\, = \frac{{5\pi }}{6} - \frac{\pi }{2} - \left( {\frac{{7\pi }}{6} - \pi } \right) - 2\left( {\frac{{3\pi }}{2} - \frac{{7\pi }}{6}} \right) \cr
& \,\,\,\,\, = - \frac{\pi }{2} \cr} $$
135.
If $$y = f\left( x \right)$$ makes $$+ve$$ intercept of $$2$$ and $$0$$ unit on $$x$$ and $$y$$ axes and encloses an area of $$\frac{3}{4}$$ square unit with the axes then, $$\int\limits_0^2 {x\,f'\left( x \right)dx} $$ is-
A
$$\frac{3}{2}$$
B
$$1$$
C
$$\frac{5}{4}$$
D
$$ - \frac{3}{4}$$
Answer :
$$ - \frac{3}{4}$$
View Solution
$$\eqalign{
& {\text{We have }}\int\limits_0^2 {f\left( x \right)dx} = \frac{3}{4}; \cr
& {\text{Now, }} \cr
& \int\limits_0^2 {x\,f'\left( x \right)dx} = x\int\limits_0^2 {f'\left( x \right)dx} - \int\limits_0^2 {f\left( x \right)dx} \cr
& = \left[ {x\,f\left( x \right)} \right]_0^2 - \frac{3}{4} = 2f\left( 2 \right) - \frac{3}{4} \cr
& = 0 - \frac{3}{4}\,\,\,\left[ {\because f\left( 2 \right) = 0} \right] \cr
& = - \frac{3}{4} \cr} $$
136.
If $$\int_0^1 {\left( {1 + {{\sin }^4}x} \right)\left( {a{x^2} + bx + c} \right)dx} = \int_0^2 {\left( {1 + {{\sin }^4}x} \right)\left( {a{x^2} + bx + c} \right)dx} $$ then the quadratic equation $$a{x^2} + bx + c = 0$$ has :
A
at least one root in (1, 2)
B
no root in (1, 2)
C
two equal roots in (1, 2)
D
both roots imaginary
Answer :
at least one root in (1, 2)
View Solution
Clearly, $$\int_1^2 {\left( {1 + {{\sin }^4}x} \right)} \left( {a{x^2} + bx + c} \right)dx = 0$$
137.
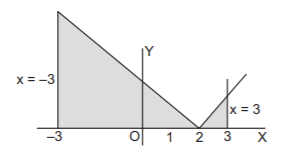
The area bounded by the lines $$y = \left| {x - 2} \right|,\,\left| x \right| = 3$$ and $$y=0$$ is :
A
$$13{\text{ uni}}{{\text{t}}^2}$$
B
$$5{\text{ uni}}{{\text{t}}^2}$$
C
$$9{\text{ uni}}{{\text{t}}^2}$$
D
$$7{\text{ uni}}{{\text{t}}^2}$$
Answer :
$$13{\text{ uni}}{{\text{t}}^2}$$
View Solution
$${\text{Area}} = \frac{1}{2}.1.1 + \frac{1}{2}.5.5.\frac{{26}}{2} = 13$$
138.
If $$\phi \left( x \right) = \int_x^{{x^2}} {\left( {t - 1} \right)dt,\,1 \leqslant x \leqslant 2,} $$ then the greatest value of $$\phi \left( x \right)$$ is :
A
2
B
4
C
8
D
none of these
Answer :
4
View Solution
$$\eqalign{
& \phi \left( x \right) = \int_0^{{x^2}} {\left( {t - 1} \right)dt} - \int_0^x {\left( {t - 1} \right)dt} \cr
& \therefore \phi '\left( x \right) = \left( {{x^2} - 1} \right).2x - \left( {x - 1} \right) = 2{x^3} - 3x + 1 \cr
& \therefore \phi '\left( x \right) = \left( {x - 1} \right)\left( {2{x^2} + 2x - 1} \right) \cr
& = 2\left( {x - 1} \right)\left( {{x^2} + x - \frac{1}{2}} \right) \cr
& = 2\left( {x - 1} \right)\left\{ {{{\left( {x + \frac{1}{2}} \right)}^2} - \frac{3}{4}} \right\} \cr} $$
139.
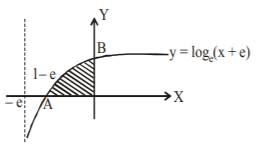
The area enclosed between the curve $$y = {\log _e}\left( {x + e} \right)$$ and the coordinate axes is :
A
1
B
2
C
3
D
4
Answer :
1
View Solution
Required area $$\left( {OAB} \right)$$
$$\eqalign{
& = \int\limits_{1 - e}^0 {\ln \left( {x + e} \right)dx} \cr
& = \left[ {x\,\ln \left( {x + e} \right) - \int {\frac{1}{{x + e}}x\,dx} } \right]_0^1 \cr
& = 1 \cr} $$
140.
$$\int_0^{\frac{\pi }{4}} {\sin \,x\,d\left( {x - \left[ x \right]} \right)} $$ is equal to :
A
$$\frac{1}{2}$$
B
$$1 - \frac{1}{{\sqrt 2 }}$$
C
1
D
none of these
Answer :
$$1 - \frac{1}{{\sqrt 2 }}$$
View Solution
$$\eqalign{
& {\text{Let }}x - \left[ x \right] = z.{\text{ In }}0 \leqslant x \leqslant \frac{\pi }{4},\,\left[ x \right] = 0.\,\,{\text{So }}x = z. \cr
& \therefore I = \int_0^{\frac{\pi }{4}} {\sin \,z\,dz} \,\, = \left[ { - \cos \,z} \right]_0^{\frac{\pi }{4}}\,\, = 1 - \frac{1}{{\sqrt 2 }} \cr} $$