121. Let $$\vec a,\,\vec b$$ and $$\vec c$$ be three unit vectors such that $$\vec a \times \left( {\vec b \times \vec c} \right) = \frac{{\sqrt 3 }}{2}\left( {\vec b + \vec c} \right).$$ If $$\vec b$$ is not parallel to $$\vec c$$ then the angle between $$\vec a$$ and $$\vec b$$ is :
A
$$\frac{{2\pi }}{3}$$
B
$$\frac{{5\pi }}{6}$$
C
$$\frac{{3\pi }}{4}$$
D
$$\frac{\pi }{2}$$
Answer :
$$\frac{{5\pi }}{6}$$
122. Let $$\overrightarrow p ,\,\overrightarrow q ,\,\overrightarrow r $$ be three mutually perpendicular vectors of the same magnitude. If a vector $$\overrightarrow x $$ satisfies the equation $$\overrightarrow p \times \left\{ {\left( {\overrightarrow x - \overrightarrow q } \right) \times \overrightarrow p } \right\} + \overrightarrow q \times \left\{ {\left( {\overrightarrow x - \overrightarrow r } \right) \times \overrightarrow q } \right\} + \overrightarrow r \times \left\{ {\left( {\overrightarrow x - \overrightarrow p } \right) \times \overrightarrow r } \right\} = \overrightarrow 0 $$ then $$\overrightarrow x $$ is given by :
A
$$\frac{1}{2}\left( {\overrightarrow p + \overrightarrow q - 2\overrightarrow r } \right)$$
B
$$\frac{1}{2}\left( {\overrightarrow p + \overrightarrow q + \overrightarrow r } \right)$$
C
$$\frac{1}{3}\left( {\overrightarrow p + \overrightarrow q + \overrightarrow r } \right)$$
D
$$\frac{1}{3}\left( {2\overrightarrow p + \overrightarrow q - \overrightarrow r } \right)$$
Answer :
$$\frac{1}{2}\left( {\overrightarrow p + \overrightarrow q + \overrightarrow r } \right)$$
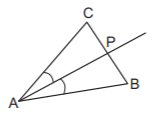
123. Let $$\overrightarrow {AB} = 3\overrightarrow i + \overrightarrow j - \overrightarrow k $$ and $$\overrightarrow {AC} = \overrightarrow i - \overrightarrow j + 3\overrightarrow k .$$ If the point $$P$$ on the line segment $$BC$$ is equidistant from $$AB$$ and $$AC$$ then $$\overrightarrow {AP} $$ is :
A
$$2\overrightarrow i - \overrightarrow k $$
B
$$\overrightarrow i - 2\overrightarrow k $$
C
$$2\overrightarrow i + \overrightarrow k $$
D
none of these
Answer :
$$2\overrightarrow i + \overrightarrow k $$
124. The position vectors of the vertices $$A,\,B,\,C$$ of a triangle are $$\overrightarrow i - \overrightarrow j - 3\overrightarrow k ,\,2\overrightarrow i + \overrightarrow j - 2\overrightarrow k $$ and $$ - 5\overrightarrow i + 2\overrightarrow j - 6\overrightarrow k $$ respectively. The length of the bisector $$AD$$ of the angle $$BAC$$ where $$D$$ is on the line segment $$BC,$$ is :
A
$$\frac{{15}}{2}$$
B
$$\frac{1}{4}$$
C
$$\frac{{11}}{2}$$
D
none of these
Answer :
$$\frac{{15}}{2}$$
125. The value of $$'a\,'$$ so that the volume of parallelepiped formed by $$\hat i + a\hat j + \hat k,\,\hat j + a\hat k$$ and $$a\hat i + \hat k$$ becomes minimum is :
A
$$ - 3$$
B
$$3$$
C
$$\frac{1}{{\sqrt 3 }}$$
D
$${\sqrt 3 }$$
Answer :
$$\frac{1}{{\sqrt 3 }}$$
126. The equation of the locus of the point $$\left( {1 + \frac{r}{4},\, - 1 + \frac{r}{3},\,2} \right),$$ where $$r\, \in \,R,$$ is given by :
A
$$\frac{{x - 1}}{4} = \frac{{y + 1}}{3} = \frac{{z - 2}}{0}$$
B
$$\frac{{x - 1}}{3} = \frac{{y + 1}}{4} = \frac{{z - 2}}{0}$$
C
$$4x - 3y = 7$$
D
$$z = 2$$
Answer :
$$\frac{{x - 1}}{3} = \frac{{y + 1}}{4} = \frac{{z - 2}}{0}$$
127. For any vector $$\overrightarrow p ,$$ the value of $$\frac{3}{2}\left\{ {{{\left| {\overrightarrow p \times \hat i} \right|}^2} + {{\left| {\overrightarrow p \times \hat j} \right|}^2} + {{\left| {\overrightarrow p \times \hat k} \right|}^2}} \right\}{\text{ is :}}$$
A
$${\overrightarrow p ^2}$$
B
$$2{\overrightarrow p ^2}$$
C
$$3{\overrightarrow p ^2}$$
D
$$4{\overrightarrow p ^2}$$
Answer :
$$3{\overrightarrow p ^2}$$
128. The number of real values of $$k$$ for which the lines $$\frac{{x - 1}}{4} = \frac{{y + 1}}{3} = \frac{z}{k}$$ and $$\frac{x}{1} = \frac{{y - k}}{3} = \frac{{z - 1}}{{ - 2}}$$ are coplanar, is :
A
2
B
1
C
3
D
0
Answer :
2
129. If the straight lines $$x = 1 + s,\,y = - 3 - \lambda s,\,z = 1 + \lambda s$$ and $$x = \frac{t}{2},\,y = 1 + t,\,z = 2 - t$$ with parameters $$s$$ and $$t$$ respectively, are co-planar, then $$\lambda $$ equals.
A
$$0$$
B
$$ - 1$$
C
$$ - \frac{1}{2}$$
D
$$ - 2$$
Answer :
$$ - 2$$
130. If $$\overrightarrow a $$ and $$\overrightarrow b $$ are unit vectors and $$\alpha $$ is the angle between them then $$\cos \frac{\alpha }{2}$$ is equal to :
A
$$\frac{1}{2}\left| {\overrightarrow a + \overrightarrow b } \right|$$
B
$$\frac{1}{2}\left| {\overrightarrow a - \overrightarrow b } \right|$$
C
$$\left| {\overrightarrow a + \overrightarrow b } \right|$$
D
none of these
Answer :
$$\frac{1}{2}\left| {\overrightarrow a + \overrightarrow b } \right|$$