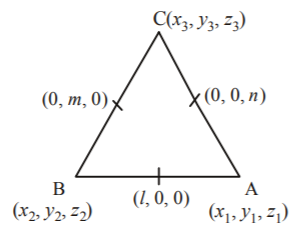131. The lines $$\frac{{x - 2}}{1} = \frac{{y - 3}}{1} = \frac{{z - 4}}{{ - k}}$$ and $$\frac{{x - 1}}{k} = \frac{{y - 4}}{1} = \frac{{z - 5}}{1}$$ are coplanar if :
A
$$k=3$$ or $$-2$$
B
$$k=0$$ or $$-1$$
C
$$k=1$$ or $$-1$$
D
$$k=0$$ or $$-3$$
Answer :
$$k=0$$ or $$-3$$
132. If the lines $$\frac{{x - 2}}{1} = \frac{{y - 3}}{1} = \frac{{z - 4}}{{ - k}}$$ and $$\frac{{x - 1}}{k} = \frac{{y - 4}}{2} = \frac{{z - 5}}{1}$$ are coplanar, then $$k$$ can have :
A
any value
B
exactly one value
C
exactly two values
D
exactly three values
Answer :
exactly two values
133. Under what condition does the equation $${x^2} + {y^2} + {z^2} + 2ux + 2vy + 2wz = 0$$ represent a real sphere ?
A
$${u^2} + {v^2} + {w^2} = {d^2}$$
B
$${u^2} + {v^2} + {w^2} > d$$
C
$${u^2} + {v^2} + {w^2} < d$$
D
$${u^2} + {v^2} + {w^2} < {d^2}$$
Answer :
$${u^2} + {v^2} + {w^2} > d$$
134. If $$O,\,P$$ are the points $$\left( {0,\,0,\,0} \right),\,\left( {2,\,3,\, - 1} \right)$$ respectively, then what is the equation to the plane through $$P$$ at right angles to $$OP\,?$$
A
$$2x + 3y + z = 16$$
B
$$2x + 3y - z = 14$$
C
$$2x + 3y + z = 14$$
D
$$2x + 3y - z = 0$$
Answer :
$$2x + 3y - z = 14$$
135. Ratio in which the $$zx$$ -plane divides the join of $$\left( {1,\,2,\,3} \right)$$ and $$\left( {4,\,2,\,1} \right).$$
A
$$1 : 1$$ internally
B
$$1 : 1$$ externally
C
$$2 : 1$$ internally
D
$$2 : 1$$ externally
Answer :
$$1 : 1$$ externally
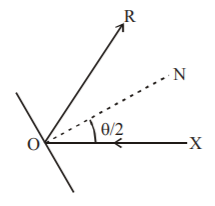
136. A mirror and a source of light are situated at the origin $$O$$ and at a point on $$OX$$ respectively. A ray of light from the source strikes the mirror and is reflected. If the direction ratios of the normal to the plane are $$1,\, – 1,\, 1,$$ then direction cosines of the reflected rays are :
A
$$\frac{1}{3},\,\frac{2}{3},\,\frac{2}{3}$$
B
$$ - \frac{1}{3},\,\frac{2}{3},\,\frac{2}{3}$$
C
$$ - \frac{1}{3},\,\frac{2}{3},\, - \frac{2}{3}$$
D
$$ - \frac{1}{3},\, - \frac{2}{3},\,\frac{2}{3}$$
Answer :
$$ - \frac{1}{3},\, - \frac{2}{3},\,\frac{2}{3}$$
137.
In $$\Delta ABC$$ the mid-point of the sides $$AB,\,BC$$ and $$CA$$ are respectively $$\left( {l,\,0,\,0} \right),\,\left( {0,\,m,\,0} \right)$$ and $$\left( {0,\,0,\,n} \right).$$
Then, $$\frac{{A{B^2} + B{C^2} + C{A^2}}}{{{l^2} + {m^2} + {n^2}}}$$ is equal to :
A
2
B
4
C
8
D
16
Answer :
8
138. Distance between two parallel planes $$2x+y+2z=8$$ and $$4x+2y+4z+5=0$$ is :
A
$$\frac{3}{2}$$
B
$$\frac{5}{2}$$
C
$$\frac{7}{2}$$
D
$$\frac{9}{2}$$
Answer :
$$\frac{7}{2}$$
139. The locus of a point, such that the sum of the squares of its distances from the planes $$x + y + z = 0,\,x - z = 0$$ and $$x - 2y + z = 0$$ is $$9$$, is :
A
$${x^2} + {y^2} + {z^2} = 3$$
B
$${x^2} + {y^2} + {z^2} = 6$$
C
$${x^2} + {y^2} + {z^2} = 9$$
D
$${x^2} + {y^2} + {z^2} = 12$$
Answer :
$${x^2} + {y^2} + {z^2} = 9$$
140. The line which passes through the origin and intersect the two lines $$\frac{{x - 1}}{2} = \frac{{y + 3}}{4} = \frac{{z - 5}}{3},\,\frac{{x - 4}}{2} = \frac{{y + 3}}{3} = \frac{{z - 14}}{4},{\text{ is :}}$$
A
$$\frac{x}{1} = \frac{y}{{ - 3}} = \frac{z}{5}$$
B
$$\frac{x}{{ - 1}} = \frac{y}{3} = \frac{z}{5}$$
C
$$\frac{x}{1} = \frac{y}{3} = \frac{z}{{ - 5}}$$
D
$$\frac{x}{1} = \frac{y}{4} = \frac{z}{{ - 5}}$$
Answer :
$$\frac{x}{1} = \frac{y}{{ - 3}} = \frac{z}{5}$$