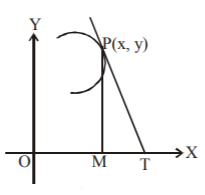1. What are the order and degree respectively of the differential equation $$y = x\frac{{dy}}{{dx}} + \frac{{dx}}{{dy}}\,?$$
A
$$1,\,1$$
B
$$1,\,2$$
C
$$2,\,1$$
D
$$2,\,2$$
Answer :
$$1,\,2$$
2. A curve is such that the portion of the $$x$$-axis cut off between the origin and the tangent at a point is twice the abscissa and which passes through the point $$\left( {1,\,2} \right).$$ The equation of the curve is :
A
$$xy = 1$$
B
$$xy = 2$$
C
$$xy = 3$$
D
none of these
Answer :
$$xy = 2$$
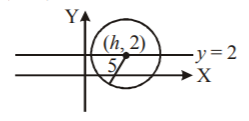
3. The differential equation of the family of circles with fixed radius $$5$$ units and centre on the line $$y = 2$$ is :
A
$$\left( {y - 2} \right)y{'^2} = 25 - {\left( {y - 2} \right)^2}$$
B
$${\left( {y - 2} \right)^2}y{'^2} = 25 - {\left( {y - 2} \right)^2}$$
C
$${\left( {x - 2} \right)^2}y{'^2} = 25 - {\left( {y - 2} \right)^2}$$
D
$$\left( {x - 2} \right)y{'^2} = 25 - {\left( {y - 2} \right)^2}$$
Answer :
$${\left( {y - 2} \right)^2}y{'^2} = 25 - {\left( {y - 2} \right)^2}$$
4. The solution of the differential equation $$\frac{{dy}}{{dx}} + \frac{y}{x}\log \,y = \frac{y}{{{x^2}}}{\left( {\log \,y} \right)^2}$$ is :
A
$$y = \log \left( {{x^2} + cx} \right)$$
B
$$\log \,y = x\left( {c{x^2} + \frac{1}{2}} \right)$$
C
$$x = \log \,y\left( {c{x^2} + \frac{1}{2}} \right)$$
D
none of these
Answer :
$$x = \log \,y\left( {c{x^2} + \frac{1}{2}} \right)$$
5. A function $$y = f\left( x \right)$$ satisfies the differential equation $$\frac{{dy}}{{dx}} - y = \cos \,x - \sin \,x$$ with initial condition that $$y$$ is bounded when $$x \to \infty .$$ The area enclosed by $$y = f\left( x \right),\,y = \cos \,x$$ and the $$y$$-axis is :
A
$$\sqrt 2 - 1$$
B
$$\sqrt 2 $$
C
$$1$$
D
$$\frac{1}{{\sqrt 2 }}$$
Answer :
$$\sqrt 2 - 1$$
6. Solution of differential equation $${x^2} = 1 + {\left( {\frac{x}{y}} \right)^{ - 1}}\frac{{dy}}{{dx}} + \frac{{{{\left( {\frac{x}{y}} \right)}^{ - 2}}{{\left( {\frac{{dy}}{{dx}}} \right)}^2}}}{{2!}} + \frac{{{{\left( {\frac{x}{y}} \right)}^{ - 3}}{{\left( {\frac{{dy}}{{dx}}} \right)}^3}}}{{3!}} + .....\,{\text{is}}\,{\text{:}}$$
A
$${y^2} = {x^2}\left( {\ln {x^2} - 1} \right) + C$$
B
$$y = {x^2}\left( {\ln x - 1} \right) + C$$
C
$${y^2} = x\left( {\ln x - 1} \right) + C$$
D
$$y = {x^2}{e^{{x^2}}} + C$$
Answer :
$${y^2} = {x^2}\left( {\ln {x^2} - 1} \right) + C$$
7. Solution of the differential equation $$ydx + \left( {x + {x^2}y} \right)dy = 0$$ is-
A
$$\log \,y = Cx$$
B
$$ - \frac{1}{{xy}} + \log \,y = C$$
C
$$\frac{1}{{xy}} + \log \,y = C$$
D
$$ - \frac{1}{{xy}} = C$$
Answer :
$$ - \frac{1}{{xy}} + \log \,y = C$$
8. The degree and order respectively of the differential equation $$\frac{{dy}}{{dx}} = \frac{1}{{x + y + 1}}$$ are :
A
$$1,\,1$$
B
$$1,\,2$$
C
$$2,\,1$$
D
$$2,\,2$$
Answer :
$$1,\,1$$
9. If $$y = y\left( x \right)$$ and it follows the relation $$x\,\cos \,y + y\,\cos \,x = \pi $$ then $$y''\left( 0 \right) = $$
A
$$1$$
B
$$-1$$
C
$$\pi - 1$$
D
$$ - \pi $$
Answer :
$$\pi - 1$$
10. What is the solution of the differential equation $$a\left( {x\frac{{dy}}{{dx}} + 2y} \right) = xy\frac{{dy}}{{dx}}\,?$$
A
$${x^2} = ky{e^{\frac{y}{a}}}$$
B
$$y{x^2} = ky{e^{\frac{y}{a}}}$$
C
$${y^2}{x^2} = ky{e^{\frac{{{y^2}}}{a}}}$$
D
none of these
Answer :
none of these