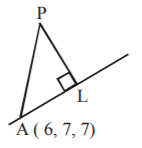1. The angle between the lines $$2x=3y=-z$$ and $$6x=-y=-4z$$ is :
A
$${0^ \circ }$$
B
$${90^ \circ }$$
C
$${45^ \circ }$$
D
$${30^ \circ }$$
Answer :
$${90^ \circ }$$
2. The equation of locus of a point whose distance from the $$y$$-axis is equal to its distance from the point $$\left( {2,\,1,\, - 1} \right)$$ is :
A
$${x^2} + {y^2} + {z^2} = 6$$
B
$${x^2} - 4x + 2z + 6 = 0$$
C
$${y^2} - 2y - 4x + 2z + 6 = 0$$
D
$${x^2} + {y^2} - {z^2} = 0$$
Answer :
$${y^2} - 2y - 4x + 2z + 6 = 0$$
3. What is the value of $$n$$ so that the angle between the lines having direction ratios $$\left( {1,\,1,\,1} \right)$$ and $$\left( {1,\, - 1,\,n} \right)$$ is $${60^ \circ }\,?$$
A
$$\sqrt 3 $$
B
$$\sqrt 6 $$
C
$$3$$
D
None of these
Answer :
$$\sqrt 6 $$
4. The perpendicular distance of $$P\left( {1,\,2,\,3} \right)$$ from the line $$\frac{{x - 6}}{3} = \frac{{y - 7}}{2} = \frac{{z - 7}}{{ - 2}}$$ is :
A
$$7$$
B
$$5$$
C
$$0$$
D
$$6$$
Answer :
$$7$$
5. A line makes $${45^ \circ }$$ with positive $$x$$-axis and makes equal angles with positive $$y,\, z$$ axes, respectively. What is the sum of the three angles which the line makes with positive $$x,\,y$$ and $$z$$ axes ?
A
$${180^ \circ }$$
B
$${165^ \circ }$$
C
$${150^ \circ }$$
D
$${135^ \circ }$$
Answer :
$${165^ \circ }$$
6. Given the line $$L:\frac{{x - 1}}{3} = \frac{{y + 1}}{2} = \frac{{z - 3}}{{ - 1}}$$ and the plane $$\pi \,:x - 2y = z.$$ Of the following assertions, the only one that is always true is :
A
$$L$$ is $$ \bot $$ to $$\pi $$
B
$$L$$ lies in $$\pi $$
C
$$L$$ is parallel to $$\pi $$
D
None of these
Answer :
$$L$$ lies in $$\pi $$
7. A plane which is perpendicular to two planes $$2x - 2y + z = 0$$ and $$x - y + 2z = 4,$$ passes through $$\left( {1,\, - 2,\,1} \right).$$ The distance of the plane from the point $$\left( {1,\,2,\,2} \right)$$ is :
A
$$0$$
B
$$1$$
C
$$\sqrt 2 $$
D
$$2\sqrt 2 $$
Answer :
$$2\sqrt 2 $$
8. The two lines $$x=ay+b,\,z=cy+d\,;$$ and $$x=a'y+b',\,z=c'y+d'$$ are perpendicular to each other if :
A
$$aa'+cc'=-1$$
B
$$aa'+cc'=1$$
C
$$\frac{a}{{a'}} + \frac{c}{{c'}} = - 1$$
D
$$\frac{a}{{a'}} + \frac{c}{{c'}} = 1$$
Answer :
$$aa'+cc'=-1$$
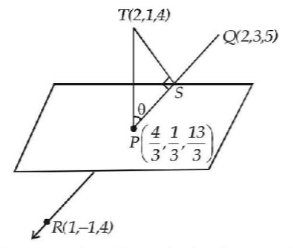
9. The point $$P$$ is the intersection of the straight line joining the points $$Q\left( {2,\,3,\,5} \right)$$ and $$R\left( {1,\, - 1,\,4} \right)$$ with the plane $$5x-4y-z=1.$$ If $$S$$ is the foot of the perpendicular drawn from the point $$T\left( {2,\,1,\,4} \right)$$ to $$QR,$$ then the length of the line segment $$PS$$ is :
A
$$\frac{1}{{\sqrt 2 }}$$
B
$$\sqrt 2 $$
C
$$2$$
D
$$2\sqrt 2 $$
Answer :
$$\frac{1}{{\sqrt 2 }}$$
10. The equation of the plane passing through the point (1, 1, 1) and perpendicular to the planes $$2x+y-2z=5$$ and $$3x-6y-2z=7,$$ is :
A
$$14x+2y-15z=1$$
B
$$14x-2y+15z=27$$
C
$$14x+2y+15z=31$$
D
$$-14x+2y+15z=3$$
Answer :
$$14x+2y+15z=31$$